
如圖,正三角形ABC的邊長為2,D,E,F分別在三邊AB,BC和CA上,且D為AB的中點, ,
,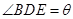 ,
,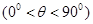 .
.
(1)當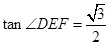 時,求
時,求 的大小;
的大小;
(2)求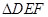 的面積S的最小值及使得S取最小值時
的面積S的最小值及使得S取最小值時 的值.
的值.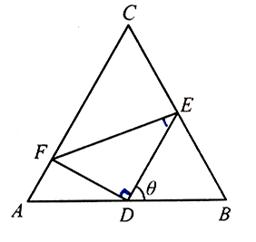
(1)θ=60°;(2)當θ=45°時,S取最小值 .
.
解析試題分析:本題主要考查正弦定理、直角三角形中正切的定義、兩角和的正弦公式、倍角公式、三角形面積公式等基礎知識,考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問,在 中,
中, ,①,而在
,①,而在 中,利用正弦定理,用
中,利用正弦定理,用 表示DE,在
表示DE,在 中,利用正弦定理,用
中,利用正弦定理,用 表示DF,代入到①式中,再利用兩角和的正弦公式展開,解出
表示DF,代入到①式中,再利用兩角和的正弦公式展開,解出 ,利用特殊角的三角函數值求角
,利用特殊角的三角函數值求角 ;第二問,將第一問得到的DF和DE代入到三角形面積公式中,利用兩角和的正弦公式和倍角公式化簡表達式,利用正弦函數的有界性確定S的最小值.
;第二問,將第一問得到的DF和DE代入到三角形面積公式中,利用兩角和的正弦公式和倍角公式化簡表達式,利用正弦函數的有界性確定S的最小值.
在△BDE中,由正弦定理得 ,
,
在△ADF中,由正弦定理得 . 4分
. 4分
由tan∠DEF= ,得
,得 ,整理得
,整理得 ,
,
所以θ=60°. 6分
(2)S=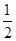 DE·DF=
DE·DF=
 . 10分
. 10分
當θ=45°時,S取最小值 . 12分
. 12分
考點:正弦定理、直角三角形中正切的定義、兩角和的正弦公式、倍角公式、三角形面積公式.


科目:高中數學 來源: 題型:解答題
如圖,有一塊正方形區域ABCD,現在要劃出一個直角三角形AEF區域進行綠化,滿足:EF=1米,設角AEF=θ,θ ,邊界AE,AF,EF的費用為每米1萬元,區域內的費用為每平方米4 萬元.
,邊界AE,AF,EF的費用為每米1萬元,區域內的費用為每平方米4 萬元.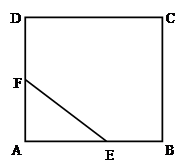
(1)求總費用y關于θ的函數.
(2)求最小的總費用和對應θ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(13分)(2011•重慶)設函數f(x)=sinxcosx﹣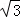 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)
(I)求f(x)的最小正周期;
(II)若函數y=f(x)的圖象按 =(
=( ,
,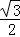 )平移后得到的函數y=g(x)的圖象,求y=g(x)在(0,
)平移后得到的函數y=g(x)的圖象,求y=g(x)在(0, ]上的最大值.
]上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示,某建筑工地準備建造一間兩面靠墻的三角形露天倉庫堆放材料,已知已有兩面墻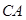 、
、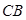 的夾角為
的夾角為 (即
(即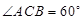 ),現有可供建造第三面圍墻的材料
),現有可供建造第三面圍墻的材料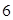 米(兩面墻的長均大于
米(兩面墻的長均大于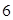 米),為了使得倉庫的面積盡可能大,記
米),為了使得倉庫的面積盡可能大,記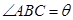 ,問當
,問當 為多少時,所建造的三角形露天倉庫的面積最大,并求出最大值?
為多少時,所建造的三角形露天倉庫的面積最大,并求出最大值? 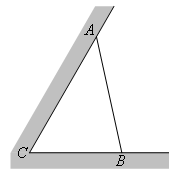
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com