已知
的三內角
、
、
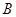所對的邊分別是
，
，
，且，，成等比數列。
（1）若
，求
的值；
（2）求角B的最大值，并判斷此時的形狀
春雨教育同步作文系列答案科目：高中數學 來源： 題型：解答題
（本題滿分14分）本題共有2個小題，第1小題滿分6分，第2小題滿分8分.
如圖，某公司要在
兩地連線上的定點
處建造廣告牌
，其中
為頂端，
長35米，
長80米，設在同一水平面上，從
和
看的仰角分別為
.
（1）設計中是鉛垂方向，若要求
，問的長至多為多少（結果精確到0.01米）？
（2）施工完成后.與鉛垂方向有偏差，現在實測得
求的長（結果精確到0.01米）？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在△ABC中，a，b，c分別是三內角A，B，C所對的三邊，已知b2＋c2＝a2＋bc．
(1)求角A的大小；
(2)若2sin2
＋2sin2
＝1，試判斷△ABC的形狀．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
（2）B的最大值為
，此時△ABC為等邊三角形
，再利用等比數列
以及余弦定理即可求出cosB的值．
，由余弦定理可得
，再由
在區間
上的單調性，
，可知△ABC為等邊三角形
，由余弦定理可得
，
，且
.
，c＝5，求b.
＝
．
的值；
中,角
的對邊分別為
,且
.
的值；
,
,求向量
在
方向上的投影.
分別為角A、B、C所對的邊，且
.
,且
，求
的值.
中，角
，
，
的對邊分別為
，
，
，若
.
；
，
時，求
中，角
所對的邊為
，且滿足
的值；
且
，求
的取值范圍．