
(1) 已知函數 ,求函數
,求函數 的最小值;
的最小值;
(2) 設x,y為正數, 且x+y=1,求 +
+ 的最小值.
的最小值.
科目:高中數學 來源: 題型:解答題
已知焦點在y軸,頂點在原點的拋物線C1經過點P(2,2),以C1上一點C2為圓心的圓過定點A(0,1),記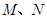 為圓
為圓 與
與 軸的兩個交點.
軸的兩個交點.
(1)求拋物線 的方程;
的方程;
(2)當圓心 在拋物線上運動時,試判斷
在拋物線上運動時,試判斷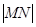 是否為一定值?請證明你的結論;
是否為一定值?請證明你的結論;
(3)當圓心 在拋物線上運動時,記
在拋物線上運動時,記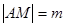 ,
, ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某商品進貨價每件50元,據市場調查,當銷售價格(每件x元)為50<x≤80時,每
天售出的件數為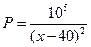 ,若要使每天獲得的
,若要使每天獲得的 利潤最多,銷售價格每件應定為多少元
利潤最多,銷售價格每件應定為多少元 ?
?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com