
已知函數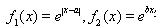
(I)若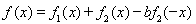 ,是否存在a,b
,是否存在a,b R,y=f(x)為偶函數.如果存在.請舉例并證明你的結論,如果不存在,請說明理由;
R,y=f(x)為偶函數.如果存在.請舉例并證明你的結論,如果不存在,請說明理由;
〔II)若a=2,b=1.求函數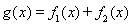 在R上的單調區(qū)間;
在R上的單調區(qū)間;
(III )對于給定的實數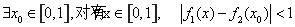 成立.求a的取值范圍.
成立.求a的取值范圍.
(I) 存在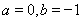 使
使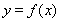 為偶函數〔II)
為偶函數〔II)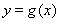 的增區(qū)間為
的增區(qū)間為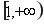 ,減區(qū)間為
,減區(qū)間為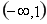 。(III )
。(III ) 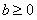 時,
時,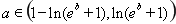 ;當
;當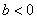 時,
時,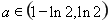
【解析】(Ⅰ)存在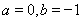 使
使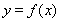 為偶函數,………………(2分)
為偶函數,………………(2分)
證明如下:此時: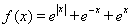 ,
,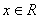
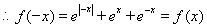 ,
,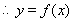 為偶函數。………………(4分)
為偶函數。………………(4分)
(注: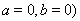 也可以)
也可以)
(Ⅱ)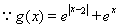 =
= ,………………(5分)
,………………(5分)
①當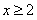 時
時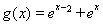 ,
,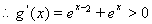
 在
在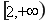 上為增函數。………………(6分)
上為增函數。………………(6分)
②當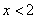 時
時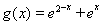 ,
,
則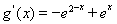 ,令
,令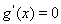 得到
得到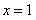 ,
,
(ⅰ)當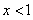 時
時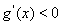 ,
,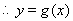 在
在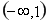 上為減函數。
上為減函數。
(ⅱ) 當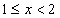 時
時 ,
,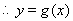 在
在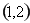 上為增函數。………………(8分)
上為增函數。………………(8分)
綜上所述: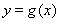 的增區(qū)間為
的增區(qū)間為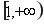 ,減區(qū)間為
,減區(qū)間為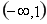 。………………(9分)
。………………(9分)
(Ⅲ)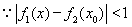 ,
,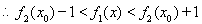
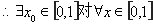 ,
,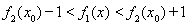 成立。
成立。
即: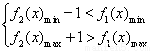 …………………………………………………(10分)
…………………………………………………(10分)
①當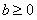 時,
時, 為增函數或常數函數,
為增函數或常數函數, 當
當 時
時
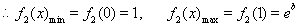
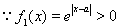
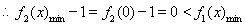 恒成立。
恒成立。
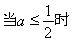

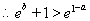
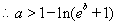
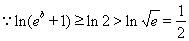
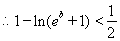
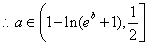
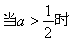
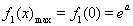
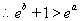
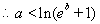
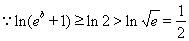
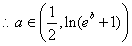
綜上所述: ……………………………………………(12分)
……………………………………………(12分)
②當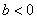 時,
時, 在[0,1]上為減函數,
在[0,1]上為減函數,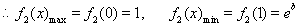
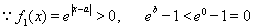
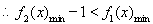 恒成立。
恒成立。
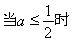

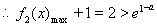
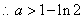

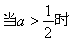
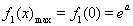

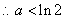
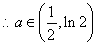
綜上所述: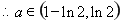 ……………………………………………(13分)
……………………………………………(13分)
由①②得當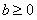 時,
時,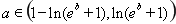 ;
;
當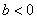 時,
時,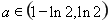 .……………………………………………(14分)
.……………………………………………(14分)


 步步高達標卷系列答案
步步高達標卷系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(yè)七十二第十章第九節(jié)練習卷(解析版) 題型:填空題
一個籃球運動員投籃一次得3分的概率為a,得2分的概率為b,不得分的概率為c,a,b,c∈(0,1),且無其他得分情況,已知他投籃一次得分的數學期望為1,則ab的最大值為 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(yè)七十七選修4-4第一節(jié)練習卷(解析版) 題型:解答題
將下列各極坐標方程化為直角坐標方程.
(1)θ= (ρ∈R). (2)ρcos2
(ρ∈R). (2)ρcos2 =1.
=1.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數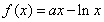 ,
,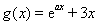 ,其中
,其中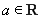 .
.
(Ⅰ)求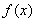 的極值;
的極值;
(Ⅱ)若存在區(qū)間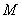 ,使
,使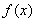 和
和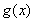 在區(qū)間
在區(qū)間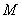 上具有相同的單調性,求
上具有相同的單調性,求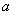 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數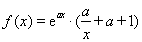 ,其中
,其中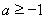 .
.
(Ⅰ)當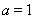 時,求曲線
時,求曲線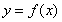 在點
在點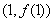 處的切線方程;
處的切線方程;
(Ⅱ)求f(x)的單調區(qū)間.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知二次函數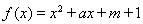 ,關于x的不等式
,關于x的不等式 的解集為
的解集為 ,其中m為非零常數.設
,其中m為非零常數.設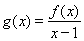 .
.
(1)求a的值;
(2)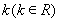 如何取值時,函數
如何取值時,函數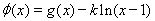 存在極值點,并求出極值點;
存在極值點,并求出極值點;
(3)若m=1,且x>0,求證: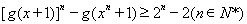
查看答案和解析>>
科目:高中數學 來源:2014年廣東省廣州市畢業(yè)班綜合測試一理科數學試卷(解析版) 題型:解答題
已知等差數列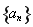 的首項為
的首項為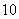 ,公差為
,公差為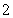 ,等比數列
,等比數列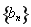 的首項為
的首項為 ,公比為
,公比為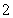 ,
,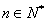 .
.
(1)求數列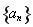 與
與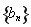 的通項公式;
的通項公式;
(2)設第 個正方形的邊長為
個正方形的邊長為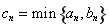 ,求前
,求前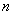 個正方形的面積之和
個正方形的面積之和 .
.
(注: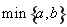 表示
表示 與
與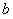 的最小值.)
的最小值.)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)仿真模擬卷2練習卷(解析版) 題型:解答題
已知f(x)=x2-2x-ln(x+1)2.
(1)求f(x)的單調遞增區(qū)間;
(2)若函數F(x)=f(x)-x2+3x+a在 上只有一個零點,求實數a的取值范圍.
上只有一個零點,求實數a的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com