(本小題滿分14分)
已知集合
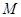
是滿足下列性質(zhì)的函數(shù)
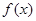
的全體, 存在非零常數(shù)
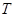
, 對任意
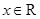
, 有
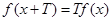
成立.
(1) 函數(shù)
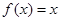
是否屬于集合
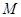
?說明理由;
(2) 設
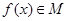
, 且
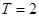
, 已知當
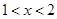
時,
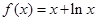
, 求當
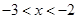
時,
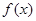
的解析式.
(3)若函數(shù)
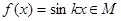
,求實數(shù)
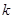
的取值范圍.
(1)
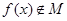
. (2)當
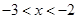
時,
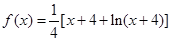
.
(3){
k|
k=
nπ,
n∈Z}
(1)假設函數(shù)
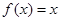
屬于集合
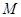
, 則存在非零常數(shù)
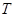
, 對任意
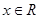
, 有
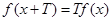
成立,即:
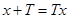
成立.在不成立的情況下,易用反例說明.因而 令
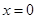
, 則
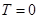
, 與題矛盾. 故
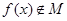
.
(2)解決本題的關鍵是
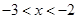
,根據(jù)1<x+4<2,從而根據(jù)
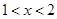
時,
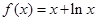
求出f(x)的表達式.
(3)解本題應討論當k=0和k≠0兩種情況.
然后解決本題的突破口是對任意
x∈R,有
f(
x+T)="T"
f(
x)成立,即sin(
kx+
kT)=Tsin
kx 因為k≠0,且
x∈R,所以
kx∈R,
kx+
kT∈R,
于是sin
kx∈[-1,1],sin(
kx+
kT) ∈[-1,1],
故要使sin(
kx+
kT)=Tsin
kx .成立,只有T=
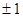
,下面再對T=1和T=-1兩種情況進行討論.
解:(1) 假設函數(shù)
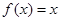
屬于集合
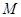
, 則存在非零常數(shù)
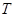
, 對任意
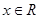
, 有
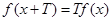
成立,
即:
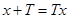
成立. 令
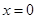
, 則
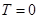
, 與題矛盾. 故
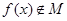
. …………5分
注:只要能判斷
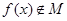
即可得1分.
(2)
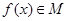
, 且
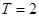
, 則對任意
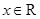
, 有
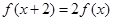
,
設
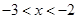
, 則
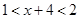
,
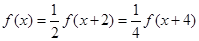
…………8分
當
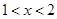
時,
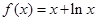
,
故當
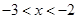
時,
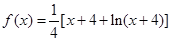
. …………10分
3)當k=0時,
f(
x)=0,顯然
f(
x)=0∈M. …………11分
當k≠0時,因為
f(
x)=sin
kx∈M,所以存在非零常數(shù)T,對任意
x∈R,有
f(
x+T)="T"
f(
x)成立,即sin(
kx+
kT)=Tsin
kx .
因為k≠0,且
x∈R,所以
kx∈R,
kx+
kT∈R,
于是sin
kx∈[-1,1],sin(
kx+
kT) ∈[-1,1],
故要使sin(
kx+
kT)=Tsin
kx .成立,只有T=
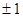
, …………12分
①當T=1時,sin(
kx+
k)=sin
kx成立,則
k=2
mπ, m∈Z .
②當T=-1時,sin(
kx-
k)=-sin
kx成立,
即sin(
kx-
k+
π)= sin
kx成立,
則-
k+
π=2
mπ, m∈Z ,即
k=-(2
m-1)
π,
m∈Z . …………13分
綜合得,實數(shù)
k的取值范圍是{
k|
k=
nπ,
n∈Z} …………14分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(16分)已知函數(shù)
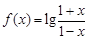
.
(1)判斷并證明
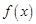
的奇偶性;
(2)求證:
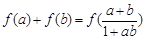
;
(3)已知a,b∈(-1,1),且
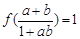
,
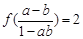
,求
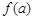
,
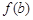
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知函數(shù)
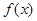
為
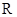
上的奇函數(shù),當
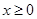
時,
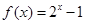
,則當
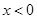
時,
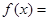
___________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)
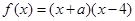
為偶函數(shù),則實數(shù)
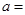
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知函數(shù)
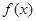
是定義在R上的奇函數(shù),
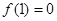
,
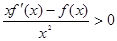
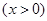
,則不等式
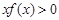
的解集是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知定義域為
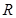
的函數(shù)
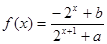
是奇函數(shù).
(1)求
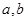
的值;
(2)若對任意的
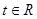
,不等式
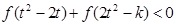
恒成立,求
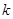
的取值范圍
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知函數(shù)
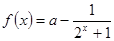
,若
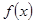
為奇函數(shù),則
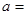
_________。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若
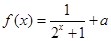
是奇函數(shù),則
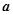
=
;
查看答案和解析>>

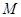 是滿足下列性質(zhì)的函數(shù)
是滿足下列性質(zhì)的函數(shù)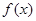 的全體, 存在非零常數(shù)
的全體, 存在非零常數(shù)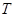 , 對任意
, 對任意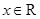 , 有
, 有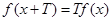 成立.
成立.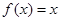 是否屬于集合
是否屬于集合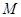 ?說明理由;
?說明理由;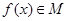 , 且
, 且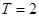 , 已知當
, 已知當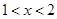 時,
時, 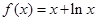 , 求當
, 求當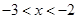 時,
時, 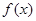 的解析式.
的解析式.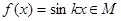 ,求實數(shù)
,求實數(shù)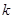 的取值范圍.
的取值范圍.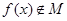 . (2)當
. (2)當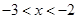 時,
時, 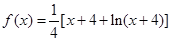 .
. 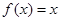 屬于集合
屬于集合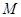 , 則存在非零常數(shù)
, 則存在非零常數(shù)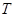 , 對任意
, 對任意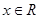 , 有
, 有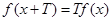 成立,即:
成立,即: 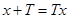 成立.在不成立的情況下,易用反例說明.因而 令
成立.在不成立的情況下,易用反例說明.因而 令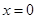 , 則
, 則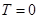 , 與題矛盾. 故
, 與題矛盾. 故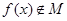 .
. 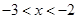 ,根據(jù)1<x+4<2,從而根據(jù)
,根據(jù)1<x+4<2,從而根據(jù)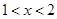 時,
時, 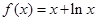 求出f(x)的表達式.
求出f(x)的表達式.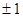 ,下面再對T=1和T=-1兩種情況進行討論.
,下面再對T=1和T=-1兩種情況進行討論.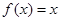 屬于集合
屬于集合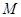 , 則存在非零常數(shù)
, 則存在非零常數(shù)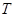 , 對任意
, 對任意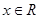 , 有
, 有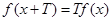 成立,
成立,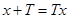 成立. 令
成立. 令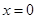 , 則
, 則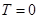 , 與題矛盾. 故
, 與題矛盾. 故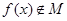 . …………5分
. …………5分 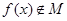 即可得1分.
即可得1分.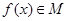 , 且
, 且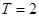 , 則對任意
, 則對任意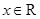 , 有
, 有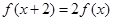 ,
,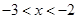 , 則
, 則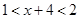 ,
, 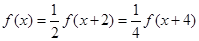 …………8分
…………8分 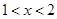 時,
時, 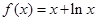 ,
, 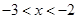 時,
時, 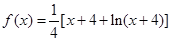 . …………10分
. …………10分 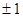 , …………12分
, …………12分

 核心素養(yǎng)學練評系列答案
核心素養(yǎng)學練評系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案