
(本題滿分12分)
設點P在曲線 上,從原點向A(2,4)移動,如果直線OP,曲線
上,從原點向A(2,4)移動,如果直線OP,曲線 及直線x=2所圍成的面積分別記為
及直線x=2所圍成的面積分別記為 、
、 。
。
(Ⅰ)當 時,求點P的坐標;
時,求點P的坐標;
(Ⅱ)當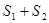 有最小值時,求點P的坐標和最小值.
有最小值時,求點P的坐標和最小值.
(1)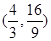 ;(2)
;(2)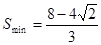 ,P點的坐標為
,P點的坐標為 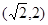 。
。
解析試題分析:(Ⅰ)設點P的橫坐標為t(0<t<2),則P點的坐標為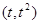 ,
,
直線OP的方程為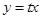 --------------2分
--------------2分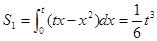 ,
,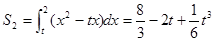 ----------6分
----------6分
因為 ,所以
,所以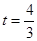 ,點P的坐標為
,點P的坐標為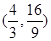 ----------7分
----------7分
(Ⅱ)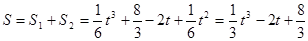 ----------8分
----------8分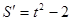 ,令S'=0得
,令S'=0得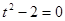 ,
,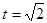 ----------9分
----------9分
因為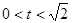 時,S'<0;
時,S'<0;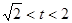 時,S'>0 ----------11分
時,S'>0 ----------11分
所以,當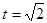 時,
時,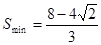 ,P點的坐標為
,P點的坐標為 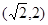 ----------12分
----------12分
考點:定積分;微積分定理;利用導數來研究函數的單調性和最值。
點評:在平常做題中,很多同學認為面積就是定積分,定積分就是面積。這里理解是錯誤的。實際上,我們是用定積分來求面積,但并不等于定積分就是面積。


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
設 ,點P(
,點P( ,0)是函數
,0)是函數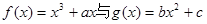 的圖象的一個公共點,兩函數的圖象在點P處有相同的切線.
的圖象的一個公共點,兩函數的圖象在點P處有相同的切線.
(1)用 表示a,b,c;
表示a,b,c;
(2)若函數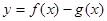 在(-1,3)上單調遞減,求
在(-1,3)上單調遞減,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數 (其中e為自然對數)
(其中e為自然對數)
(1)求F(x)="h" (x) 的極值。
的極值。
(2)設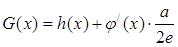 (常數a>0),當x>1時,求函數G(x)的單調區間,并在極值存在處求極值。
(常數a>0),當x>1時,求函數G(x)的單調區間,并在極值存在處求極值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)
已知函數f(x)=lnx+
(Ⅰ)求函數f(x)的單調區間;
(Ⅱ)設m R,對任意的a∈(-l,1),總存在xo∈[1,e],使得不等式ma - (xo)<0成立,求實數m的取值范圍;
R,對任意的a∈(-l,1),總存在xo∈[1,e],使得不等式ma - (xo)<0成立,求實數m的取值范圍;
(Ⅲ)證明:ln2 l+ 1n22,+…+ln2 n> ∈N*).
∈N*).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數 ,
,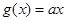 ,
,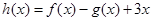 ,其中
,其中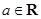 且
且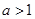 .
.
(I)求函數 的導函數
的導函數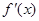 的最小值;
的最小值;
(II)當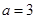 時,求函數
時,求函數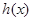 的單調區間及極值;
的單調區間及極值;
(III)若對任意的 ,函數
,函數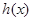 滿足
滿足 ,求實數
,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com