
(本小題12分)定義運算: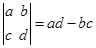
(1)若已知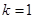 ,解關于
,解關于 的不等式
的不等式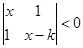
(2)若已知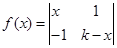 ,對任意
,對任意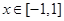 ,都有
,都有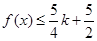 ,求實數(shù)
,求實數(shù)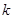 的取值范圍。
的取值范圍。
((1) ;(2)
;(2) .
.
解析試題分析:(1)當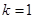 時,根據(jù)定義有
時,根據(jù)定義有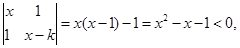

所以原不等式的解集為
(2)依題意知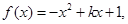
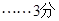
因為對任意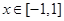 ,都有
,都有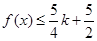 ,
,
所以
因為 的圖像開口向下,對稱軸為直線
的圖像開口向下,對稱軸為直線
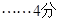
① 若 ,即
,即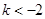 ,則
,則 在
在 為減函數(shù),
為減函數(shù),
所以 ,解得
,解得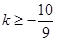 ,所以
,所以
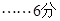
② 若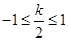 ,即
,即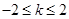 ,則
,則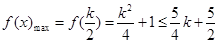 ,
,
解得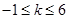 ,所以
,所以

③ 若 ,即
,即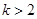 ,則
,則 在
在 為增函數(shù),
為增函數(shù),
所以 ,解得
,解得 ,所以
,所以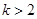

綜上所述,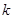 的取值范圍是
的取值范圍是

考點:本題主要以新定義為背景,考查恒成立問題.
點評:對于此類新定義問題,學生要注意仔細審題,冷靜思考,新問題的解決還是要靠“老知識”“老方法”,應該有意識地運用轉化思想,將新問題轉化為我們熟知的問題。對于恒成立問題,要轉為為求最值來解決,分情況討論求最值時,要做到不重不漏.


 期末1卷素質(zhì)教育評估卷系列答案
期末1卷素質(zhì)教育評估卷系列答案科目:高中數(shù)學 來源: 題型:解答題
(本題滿分15分)已知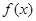 在定義域上是奇函數(shù),且在
在定義域上是奇函數(shù),且在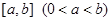 上是減函數(shù),圖像如圖所示.
上是減函數(shù),圖像如圖所示.
(1)化簡: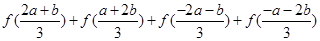 ;
;
(2)畫出函數(shù)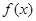 在
在 上的圖像;
上的圖像;
(3)證明: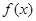 在
在 上是減函數(shù).
上是減函數(shù).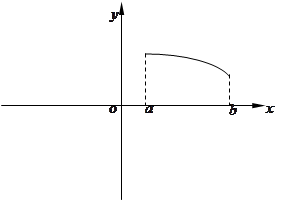
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) 的定義域為
的定義域為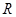 ,對于任意的
,對于任意的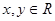 ,都有
,都有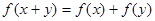 ,且當
,且當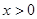 時,
時,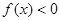 ,若
,若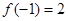 .
.
(1)求證: 為奇函數(shù);
為奇函數(shù);
(2)求證: 是
是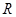 上的減函數(shù);
上的減函數(shù);
(3)求函數(shù) 在區(qū)間
在區(qū)間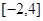 上的值域.
上的值域.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(10分)已知函數(shù)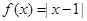
(1)用分段函數(shù)的形式表示該函數(shù);
(2)在坐標系中畫出該函數(shù)的圖像
(3)寫出該函數(shù)的定義域,值域,奇偶性和單調(diào)區(qū)間(不要求證明)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) .
.
(I)求證:不論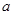 為何實數(shù)
為何實數(shù) 總是為增函數(shù);
總是為增函數(shù);
(II)確定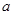 的值, 使
的值, 使 為奇函數(shù);
為奇函數(shù);
(Ⅲ)當 為奇函數(shù)時, 求
為奇函數(shù)時, 求 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)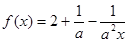 ,(
,(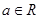 且
且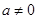 )。
)。
(1)設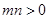 ,令
,令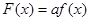 ,試判斷函數(shù)
,試判斷函數(shù)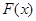 在
在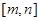 上的單調(diào)性并證明你的結論;
上的單調(diào)性并證明你的結論;
(2)若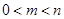 且
且
 的定義域和值域都是
的定義域和值域都是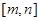 ,求
,求 的最大值;
的最大值;
(3)若不等式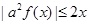 對
對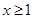 恒成立,求實數(shù)
恒成立,求實數(shù)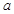 的取值范圍;
的取值范圍;
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com