
已知數列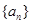 的前
的前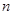 項和為
項和為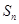 ,對一切正整數
,對一切正整數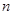 ,點
,點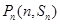 都在函數
都在函數 的圖像上,且過點
的圖像上,且過點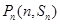 的切線的斜率為
的切線的斜率為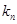 .
.
(1)求數列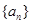 的通項公式;
的通項公式;
(2)設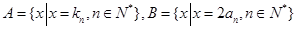 ,等差數列
,等差數列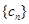 的任一項
的任一項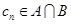 ,其中
,其中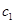 是
是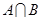 中所有元素的最小數,
中所有元素的最小數,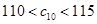 ,求
,求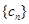 的通項公式.
的通項公式.
(1)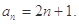 ;(2)
;(2)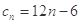
解析試題分析:(1)由于點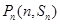 都在函數
都在函數 的圖像上,所以可得
的圖像上,所以可得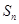 關于
關于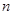 的關系式.再根據通項與前
的關系式.再根據通項與前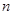 項和的關系式可求得通項.
項和的關系式可求得通項.
(2)由過點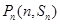 的切線的斜率為
的切線的斜率為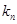 ,所以可得集合A,由(1)的結論可得集合B. 因為等差數列
,所以可得集合A,由(1)的結論可得集合B. 因為等差數列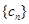 的任一項
的任一項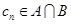 ,其中
,其中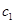 是
是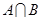 中所有元素的最小數.即可得
中所有元素的最小數.即可得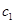 .再根據
.再根據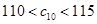 ,即可求出公差的值.從而可求得數列
,即可求出公差的值.從而可求得數列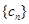 的通項公式.
的通項公式.
試題解析:(1)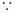 點
點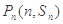 都在函數
都在函數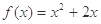 的圖像上,
的圖像上,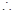
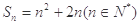 ,
,
當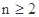 時,
時,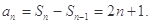
當n=1時,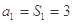 滿足上式,所以數列
滿足上式,所以數列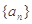 的通項公式為
的通項公式為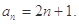
(2)由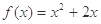 求導可得
求導可得
過點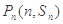 的切線的斜率為
的切線的斜率為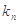 ,
,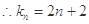 .
.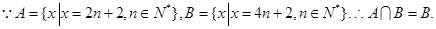 又因為
又因為 ,其中
,其中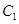 是
是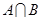 中的最小數.所以
中的最小數.所以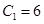 .
.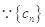 是公差是4的倍數,
是公差是4的倍數,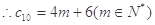
又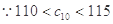 ,
,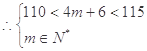 ,解得m=27.
,解得m=27.
所以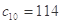 ,設等差數列的公差為
,設等差數列的公差為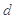 ,則
,則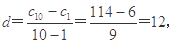
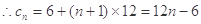 ,所以
,所以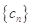 的通項公式為
的通項公式為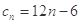
考點:1.函數的導數.2.數列的通項公式的求法.3.集合的運算.4.最值問題.


科目:高中數學 來源: 題型:解答題
如圖,半徑為30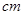 的圓形(
的圓形( 為圓心)鐵皮上截取一塊矩形材料
為圓心)鐵皮上截取一塊矩形材料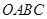 ,其中點
,其中點 在圓弧上,點
在圓弧上,點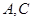 在兩半徑上,現將此矩形材料卷成一個以
在兩半徑上,現將此矩形材料卷成一個以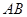 為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),設
為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),設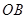 與矩形材料的邊
與矩形材料的邊 的夾角為
的夾角為 ,圓柱的體積為
,圓柱的體積為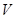
 .
.
(1)求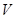 關于
關于 的函數關系式?
的函數關系式?
(2)求圓柱形罐子體積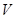 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數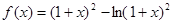 ,
,
(1)求函數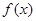 的單調區間;
的單調區間;
(2)若當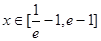 時,不等式
時,不等式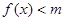 恒成立,求實數
恒成立,求實數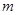 的取值范圍;
的取值范圍;
(3)若關于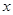 的方程
的方程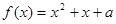 在區間
在區間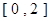 上恰好有兩個相異的實根,求實數
上恰好有兩個相異的實根,求實數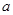 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設f(x)=ax3+bx+c(a≠0)為奇函數,其圖象在點(1,f(1))處的切線與直線x-6y-7=0垂直,導函數f′(x)的最小值為-12.
(1)求函數f(x)的解析式;
(2)求函數f(x)的單調增區間,并求函數f(x)在[-1,3]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個圓柱形圓木的底面半徑為1m,長為10m,將此圓木沿軸所在的平面剖成兩個部分.現要把其中一個部分加工成直四棱柱木梁,長度保持不變,底面為等腰梯形 (如圖所示,其中O為圓心,
(如圖所示,其中O為圓心,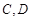 在半圓上),設
在半圓上),設 ,木梁的體積為V(單位:m3),表面積為S(單位:m2).
,木梁的體積為V(單位:m3),表面積為S(單位:m2).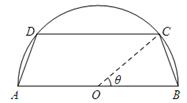
(1)求V關于θ的函數表達式;
(2)求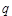 的值,使體積V最大;
的值,使體積V最大;
(3)問當木梁的體積V最大時,其表面積S是否也最大?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com