
(本小題共9分)
已知函數f(x)=Asin( x+
x+ )(x∈R,
)(x∈R, >0,0<
>0,0< <
< )的部分圖象如圖所示。
)的部分圖象如圖所示。
(Ⅰ)求函數f(x)的解析式;
(Ⅱ)求函數g(x)=f(x- )的單調遞增區間。
)的單調遞增區間。
(1) f(x)=2sin(2x+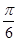 )
)
(2) g(x)的單調遞增區間是[k -
-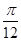 ,k
,k +
+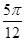 ],k∈z.
],k∈z.
解析試題分析:解:(Ⅰ)由題設圖象知,周期T=2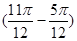 =
= ,所以
,所以 =
=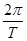 =2,
=2,
因為點(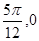 )在函數圖象上,所以Asin(2×
)在函數圖象上,所以Asin(2×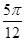 +
+ )=0,即sin(
)=0,即sin( +
+ )=0。
)=0。
又因為0< <
< ,所以
,所以 <
< +
+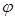 <
<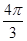 ,從而
,從而 +
+ =
= ,即
,即 =
=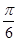 .
.
又點(0,1)在函數圖象上,所以Asin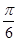 =1,A=2.
=1,A=2.
故函數f(x)的解析式為f(x)=2sin(2x+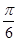 ). 5分
). 5分
(Ⅱ)g(x)=2sin[2(x- +
+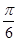 ]=2sin(2x-
]=2sin(2x- ),
),
由2k -
- ≤2x-
≤2x- ≤2k
≤2k +
+ ,得k
,得k -
-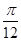 ≤x≤k
≤x≤k +
+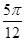 ,k∈z.
,k∈z.
所以g(x)的單調遞增區間是[k -
-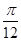 ,k
,k +
+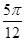 ],k∈z. 9分
],k∈z. 9分
考點:三角函數的性質
點評:對于三角函數解析式的求解,主要是根據圖像來得到周期,以及振幅,和初相的值,同時根據三角函數性質來解答,屬于基礎題。


科目:高中數學 來源: 題型:解答題
(8分)已知函數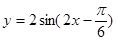 .
.
(1)寫出它的振幅、周期、頻率和初相;
(2)求這個函數的單調遞減區間;
(3)求出使這個函數取得最大值時,自變量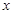 的取值集合,并寫出最大值。
的取值集合,并寫出最大值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com