
已知等比數列 中各項均為正,有
中各項均為正,有 ,
, ,
,
等差數列 中,
中, ,點
,點 在直線
在直線 上.
上.
(1)求 和
和 的值;(2)求數列
的值;(2)求數列 ,
, 的通項
的通項 和
和 ;
;
(3)設 ,求數列
,求數列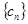 的前n項和
的前n項和 .
.
科目:高中數學 來源: 題型:填空題
① 是數列
是數列 的前
的前 項和,若
項和,若 ,則數列
,則數列 是等差數列
是等差數列
②若 ,則
,則
③已知函數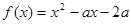 ,若存在
,若存在 ,使得
,使得 成立,則
成立,則
④在 中,
中, 分別是角A、B、C的對邊,若
分別是角A、B、C的對邊,若 則
則 為等腰直角三角形
為等腰直角三角形
其中正確的有 (填上所有正確命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校高一學生1000人,每周一次同時在兩個可容納600人的會議室,開設“音樂欣賞”與“美術鑒賞”的校本課程.要求每個學生都參加,要求第一次聽“音樂欣賞”課的人數為
 ,其余的人聽“美術鑒賞”課;從第二次起,學生可從兩個課中自由選擇.據往屆經驗,凡是這一次選擇“音樂欣賞”的學生,下一次會有20﹪改選“美術鑒賞”,而選“美術鑒賞”的學生,下次會有30﹪改選“音樂欣賞”,用
,其余的人聽“美術鑒賞”課;從第二次起,學生可從兩個課中自由選擇.據往屆經驗,凡是這一次選擇“音樂欣賞”的學生,下一次會有20﹪改選“美術鑒賞”,而選“美術鑒賞”的學生,下次會有30﹪改選“音樂欣賞”,用 分別表示在第
分別表示在第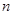 次選“音樂欣賞”課的人數和選“美術鑒賞”課的人數.
次選“音樂欣賞”課的人數和選“美術鑒賞”課的人數.
(1)若 ,分別求出第二次,第三次選“音樂欣賞”課的人數
,分別求出第二次,第三次選“音樂欣賞”課的人數 ;
;
(2)①證明數列 是等比數列,并用
是等比數列,并用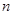 表示
表示 ;
;
②若要求前十次參加“音樂欣賞”課的學生的總人次不超過5800,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知{an}是一個公差大于0的等差數列,且滿足a4a5=55,a3+a6=16
(1)求數列{an}的通項公式;
(2)若數列{an}和數列{bn}滿足等式:
an-1= ,an=
,an= (
(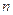 為正整數),
為正整數),
設數列{bn}的前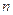 項和
項和 ,cn=(an+19)(Sn+50),數列{cn}前n項和為Tn,
,cn=(an+19)(Sn+50),數列{cn}前n項和為Tn,
求Tn的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
稱滿足以下兩個條件的有窮數列 為
為 階“期待數列”:
階“期待數列”:
① ;②
;② .
.
(1)若等比數列 為
為 階“期待數列”,求公比q及
階“期待數列”,求公比q及 的通項公式;
的通項公式;
(2)若一個等差數列 既是
既是 階“期待數列”又是遞增數列,求該數列的通項公式;
階“期待數列”又是遞增數列,求該數列的通項公式;
(3)記n階“期待數列”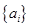 的前k項和為
的前k項和為 :
:
(i)求證: ;
;
(ii)若存在 使
使 ,試問數列
,試問數列 能否為n階“期待數列”?若能,求出所有這樣的數列;若不能,請說明理由.
能否為n階“期待數列”?若能,求出所有這樣的數列;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com