
已知函數 ,其中
,其中 .
.
(1)若 時,記
時,記 存在
存在 使
使 成立,求實數
成立,求實數 的取值范圍;
的取值范圍;
(2)若 在
在 上存在最大值和最小值,求
上存在最大值和最小值,求 的取值范圍.
的取值范圍.
⑴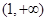 ;⑵
;⑵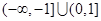
解析試題分析:⑴由已知先寫出 湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區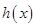 ,
,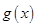 的解析式,然后根據函數的單調性與導函數的關系分別求出
的解析式,然后根據函數的單調性與導函數的關系分別求出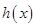 的最大值和
的最大值和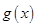 的最小值,只要使得最大值大于最小值,就能保證題設的條件成立;⑵函數的解析式中含有參數,所以做關于函數解析式的討論時一定要討論參數的取值,本題關于參數
的最小值,只要使得最大值大于最小值,就能保證題設的條件成立;⑵函數的解析式中含有參數,所以做關于函數解析式的討論時一定要討論參數的取值,本題關于參數 分三種情況進行討論,利用導數討論函數的單調性,利用導數討論函數的最值,解題時注意要全面討論,不能漏解.
分三種情況進行討論,利用導數討論函數的單調性,利用導數討論函數的最值,解題時注意要全面討論,不能漏解.
試題解析:(1)由已知得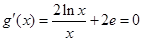 解得
解得 ,
,
當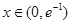 時,
時,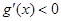 ,
,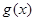 單調遞減;當
單調遞減;當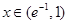 時,
時,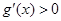 ,
,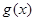 單調遞增,
單調遞增,
所以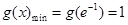 , 3分
, 3分
又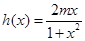 顯然
顯然 則
則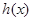 在
在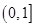 上是遞增函數,
上是遞增函數,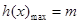 ,所以
,所以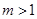 ,
,
存在 使
使 成立,實數
成立,實數 的取值范圍是
的取值范圍是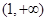 ; .6分
; .6分
(2)解: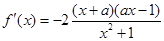 ,分類討論:
,分類討論:
①當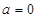 時,
時, ,
,
所以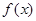 在
在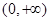 單調遞增,在
單調遞增,在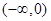 單調遞減,
單調遞減, 在
在 只有最小值沒有最大值,..8分
只有最小值沒有最大值,..8分
當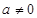 ,
,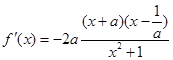 ;
;
②當 時,令
時,令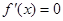 ,得
,得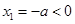 ,
,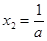 ,
, 與
與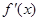 的情況如下:
的情況如下: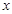
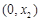
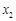
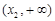
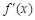



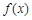
↗


智樂文化中考全真模擬試卷尖子生熱身用系列答案
超能學典中考高分突破系列答案
逗號圖書中考壓軸題專練系列答案
中教聯中考金卷中考試題精編系列答案
創新教育中考真題解析卷系列答案
中考全真模擬測試卷系列答案
通城學典全國中考試題分類精粹系列答案
金星教育中考奪冠搶分練系列答案
大中考學法大視野光明日報出版社系列答案
萬唯教育中考解答題專項集訓系列答案
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號