（12分）函數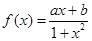
是定義域在（－1，1）上奇函數，且
.
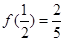（1）確定函數
的解析式；
（2）用定義證明在（－1，1）上是增函數；
（3）解不等式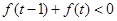
.
科目：高中數學 來源： 題型：解答題
已知平面上的線段l及點P，在l上任取一點Q，線段PQ長度的最小值稱為點P到線段l的距離，記作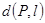
。
（1）已知點
，線段
，求；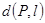
（2）設A（－1，0），B（1，0），求點集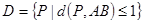
所表示圖形的面積；
（3）若M（0，1），O（0，0），N（2，0），畫出集合
所表示的圖形。（本題滿分14分）
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某公司為了實現1000萬元利潤的目標，準備制定一個激勵銷售人員的獎勵方案：在銷售利潤達到10萬元時，按銷售利潤進行獎勵，且獎金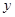
（單位：萬元）隨銷售利潤
（單位：萬元）的增加而增加，但獎金總數不超過5萬元，同時獎金不能超過利潤的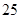
％.現有三個獎勵模型：
，分析與推導哪個函數模型能符合該公司的要求？并給予證明．（注：
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
(2) 
， 
＝
.
∴
，解得
定義在R上的偶函數，當
時，
的函數
同時滿足：
，總有
； ②
；
，則有
成立。
的值；
，總有
恒成立，求實數
的取值范圍。
，且
,定義在區間
內的函數
是奇函數.
的取值范圍；
的單調性并證明.
是R上的偶函數，且當
時，函數解析式為
,
的值；
時，函數的解析式。
為偶函數，且在區間
上是單調遞減函數，
的解析式；
的奇偶性。 （12分）
在
上的單調性.