
題目列表(包括答案和解析)
3.下列說法錯誤的是
(A)命題“若x2-3x+2=0,則x=1”的逆否命題為:“若x≠1,則x2-3x+2≠0”
(B)“x=1”是“x2-3x+2=0”的充分不必要條件
(C)若pÙq為假命題,則p、q均為假命題
(D)對于命題p:“存在x∈R,使得x2+x+1<0”,則Øp:“任意x∈R,均有x2+x+1≥0”
2.不等式y≤3x+b所表示的區(qū)域恰好使點(3,4)不在此區(qū)域內(nèi),而點(4,4)在此區(qū)域內(nèi),則b的取值范圍是
(A)-8≤b≤-5 (B)b≤-8或b>-5 (C)-8≤b<-5 (D)b≤-8或b≥-5
1.已知復數(shù)z1=3+i,z2=1-i,則復數(shù)z1·z2的虛部為
(A)2i (B)-2i (C)2 (D)-2
22. (1)證明:由g(x)=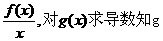 ′(x)=
′(x)=
由xf′(x)>f(x)可知:g′(x) >0在x>0上恒成立.
從而g(x)=
(2)由(1)知g(x)=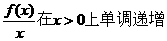
在x1>0,x2>0時,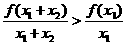
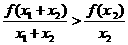
于是f(x1)<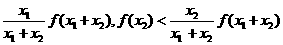
兩式相加得到:f(x1)+f(x2)<f(x1+x2)
(1)
由(2)中可知:g(x)=

由數(shù)學歸納法可知:xi>0(i=1,2,3,…,n)時,
有f(x1)+f(x2)+f(x3)+… +f(xn)<f(x1+x2+x3+…+xn) (n≥2)恒成立.
設(shè)f(x)=xlnx,則在xi>0(i=1,2,3,…,n)時
有x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+…+xn)ln(x1+x2+…+xn)(n≥2)……(*)恒成立.
令xn=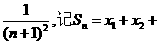 …+xn=
…+xn=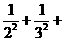 …+
…+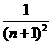
由Sn< …+
…+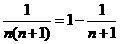
Sn>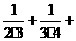 …+
…+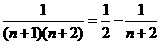
(x1+x2+…+xn)ln(x1+x2+…+xn)<(x1+x2+…+xn)ln(1-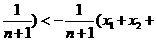 …+xn)(∵ln(1+x)<x)
…+xn)(∵ln(1+x)<x)
<-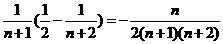 (**)
(**)
由(**)代入(*)中,可知:
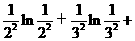 …+
…+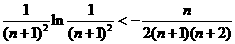
于是: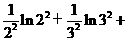 …+
…+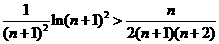
21. 解(Ⅰ)由題意,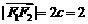 , ∴
, ∴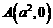 ,
2分
,
2分
∵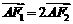 ∴
∴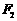 為A
為A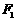 的中點
3分
的中點
3分
∴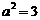 ,
,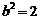
即 橢圓方程為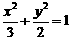 .
5分
.
5分
(Ⅱ)當直線DE與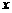 軸垂直時,
軸垂直時,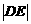
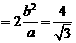 ,
,
此時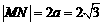 ,四邊形
,四邊形 的面積為
的面積為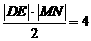 .
.
同理當MN與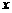 軸垂直時,也有四邊形
軸垂直時,也有四邊形 的面積為
的面積為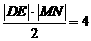 . 當直線DE,MN均與
. 當直線DE,MN均與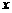 軸不垂直時,設(shè)
軸不垂直時,設(shè)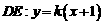 ,代入橢圓方程,消去
,代入橢圓方程,消去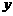 得:
得:
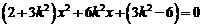 .
.
設(shè) ,
,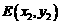 ,則
,則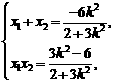 所以,
所以,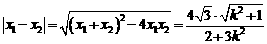 ,
,
所以,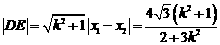 ,
,
同理,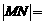
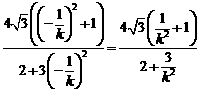 .
所以,四邊形的面積
.
所以,四邊形的面積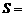
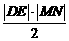 =
=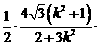
 =
=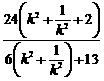 ,
,
令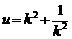 ,得
,得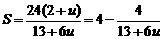
因為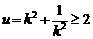 ,
,
當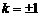 時,
時,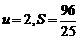 ,且S是以
,且S是以 為自變量的增函數(shù),
為自變量的增函數(shù),
所以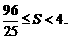
綜上可知,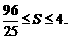 即四邊形DMEN面積的最大值為4,最小值為
即四邊形DMEN面積的最大值為4,最小值為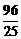 .
.
20. 解:(Ⅰ)密碼中不同數(shù)字的個數(shù)為2的事件為密碼中只有兩個數(shù)字,注意到密碼的第1,2列分別總是1,2,即只能取表格第1,2列中的數(shù)字作為密碼.
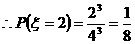 .
……………………………4分
.
……………………………4分
(Ⅱ)由題意可知, 的取值為2,3,4三種情形.
的取值為2,3,4三種情形.
若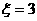 ,注意到表格的第一排總含有數(shù)字1,第二排總含有數(shù)字2則密碼中只可能取數(shù)字1,2,3或1,2,4.
,注意到表格的第一排總含有數(shù)字1,第二排總含有數(shù)字2則密碼中只可能取數(shù)字1,2,3或1,2,4.
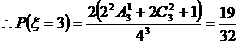 .
.
若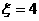 ,則
,則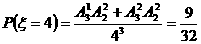
(或用 求得).
……………………………8分
求得).
……………………………8分
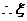 的分布列為:
的分布列為:
 |
2 |
3 |
4 |
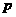 |
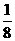 |
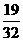 |
 |
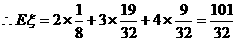 . ……………………………12分
. ……………………………12分
19. 解:(Ⅰ)由f(x)=x3+ax2+bx+c關(guān)于點(1,1)成中心對稱,所以
x3+ax2+bx+c+(2-x)3+a(2-x)2+b(2-x)+c=2
對一切實數(shù)x恒成立.得:a=-3,b+c=3,
對由f '(1)=0,得b=3,c=0,
故所求的表達式為:f(x)= x3-3x2+3x.
(Ⅱ) an+1=f (an)= an 3-3 an 2+3 an (1)
令bn=an-1,0<bn<1,由代入(1)得:bn+1=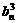 ,bn=
,bn= ,∴ 1>bn >bn+1 >0
,∴ 1>bn >bn+1 >0
(a1-a2)·(a3-1)+(a2-a3)·(a4-1)+…+(an-an+1)·(an+2-1)=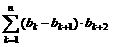
<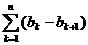 =b1-bn+1<b1<1。
=b1-bn+1<b1<1。
(本題證法較多,其它證明方法得分可參照以上評分標準分步給分)
18. 解法一:
(Ⅰ) 過P作MN∥B1C1,分別交A1B1、D1C1于M、N,則M、N A1B1、D1C1的中點,連MB,NC由四邊形BCNM是平行四邊形, ∵E、M分別為AB、A1B1中點,∴A1E∥MB
又MB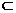 平面PBC,∴A1E∥平面PBC。
平面PBC,∴A1E∥平面PBC。
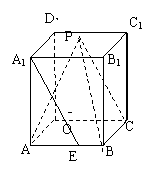 (Ⅱ) 過A作AF⊥MB,垂足為F,連PF,
(Ⅱ) 過A作AF⊥MB,垂足為F,連PF,
∵BC⊥平面ABB1A1,AF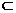 平面ABB1A1,
平面ABB1A1,
∴AF⊥BC, BC∩MB=B,∴AF⊥平面PBC,
∴∠APF就是直線AP與平面PBC所成的角,
設(shè)AA1=a,則AB= a,AF=
a,AF=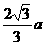 ,AP=
,AP=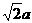 ,sin∠APF=
,sin∠APF=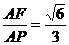
所以,直線AP與平面PBC所成的角是arcsin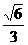 。
(Ⅲ)連OP、OB、OC,則OP⊥BC,由三垂線定理易得OB⊥PC,OC⊥PB,所以O(shè)在平面PBC中的射影是△PBC的垂心,又O在平面PBC中的射影是△PBC的重心,則△PBC為正三角形。即PB=PC=BC
所以k=
。
(Ⅲ)連OP、OB、OC,則OP⊥BC,由三垂線定理易得OB⊥PC,OC⊥PB,所以O(shè)在平面PBC中的射影是△PBC的垂心,又O在平面PBC中的射影是△PBC的重心,則△PBC為正三角形。即PB=PC=BC
所以k=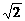 。
。
反之,當k=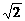 時,PA=AB=PB=PC=BC,所以三棱錐
時,PA=AB=PB=PC=BC,所以三棱錐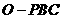 為正三棱錐,
為正三棱錐,
∴O在平面PBC內(nèi)的射影為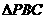 的重心
的重心 解法二:(建立空間坐標系)
解法二:(建立空間坐標系)
17.解:由題設(shè)y=cos[ (x-a)+
(x-a)+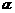 ]的圖象關(guān)于點(a+l,0)對稱,
]的圖象關(guān)于點(a+l,0)對稱,
則cos[ (a+1-a)+
(a+1-a)+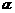 ]=0,即
]=0,即 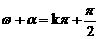 (k∈Z).……………………3分
(k∈Z).……………………3分
又f (x) =cos( x+
x+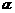 )在[
)在[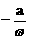 ,1]上是單調(diào)函數(shù),
,1]上是單調(diào)函數(shù),
令t= x+
x+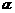 ,則g(t)= cos t在[0,
,則g(t)= cos t在[0, +
+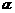 ]上是單調(diào)函數(shù),
]上是單調(diào)函數(shù),
∴0<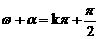 ≤
≤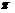 ,∴0<k+
,∴0<k+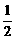 ≤1.
≤1.
∵k∈Z,∴k=0,于是  +
+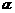 =
=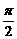 ………………………………………8分
………………………………………8分
又f (x) =cos( x+
x+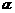 )的圖象關(guān)于點(4,0)對稱,
)的圖象關(guān)于點(4,0)對稱,
∴4 +
+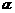
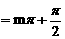 (m∈Z),∴
(m∈Z),∴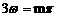 (m∈Z). ……………… 11分
(m∈Z). ……………… 11分
∵0< <
<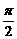 ,∴
,∴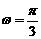 ,∴f(x)=cos(
,∴f(x)=cos(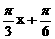 ).……………………………12分
).……………………………12分
16. 解析:設(shè)C的坐標為C(x,y),則AC中點為M(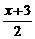 ,
,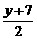 ),BC中點為N(
),BC中點為N(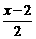 ,
,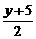 ).
).
∵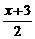 ≠
≠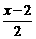 ,
,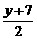 ≠
≠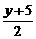 ,且AC、BC的中點M、N都在坐標軸上,
,且AC、BC的中點M、N都在坐標軸上,
∴M、N不在同一坐標軸上.
當M在x軸上、N在y軸上時,yN=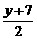 =0,xM=
=0,xM=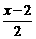 =0,
=0,
即x=2,y=-7;
當M在y軸上、N在x軸上時,xM=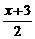 =0,yN=
=0,yN=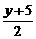 =0,
=0,
即x=-3,y=-5.
∴C點坐標為(-3,-5)或(2,-7).
答案:(-3,-5)或(2,-7)
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com