
已知函數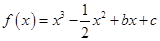 ,且
,且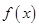 在
在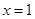 處取得極值.
處取得極值.
(1)求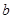 的值;
的值;
(2)若當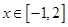 時,
時,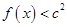 恒成立,求
恒成立,求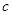 的取值范圍;
的取值范圍;
(3)對任意的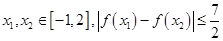 是否恒成立?如果成立,給出證明,如果不成立,請說明理由.
是否恒成立?如果成立,給出證明,如果不成立,請說明理由.
(1)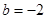 (2)
(2)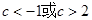 (3)不等式恒成立,證明:當
(3)不等式恒成立,證明:當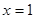 時,
時,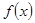 有極小值
有極小值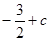 又
又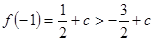 ∴
∴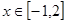 時,
時,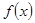 最小值為
最小值為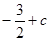
∴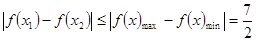 ,故結論成立.
,故結論成立.
解析試題分析:(1)
科目:高中數學
來源:
題型:解答題
(本小題滿分12分)
科目:高中數學
來源:
題型:解答題
(本題滿分12分)
科目:高中數學
來源:
題型:解答題
(14分)已知函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
∵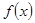 在
在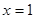 處取得極值,
處取得極值,
∴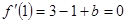
∴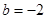 經檢驗,符合題意.
經檢驗,符合題意.
(2)∵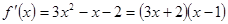

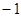
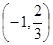
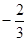




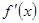
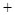

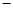

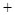
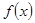
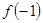

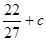

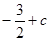



暑假生活江西高校出版社系列答案
暑假作業貴州人民出版社系列答案
暑假作業教育科學出版社系列答案
新課標暑假作業二十一世紀出版社系列答案
暑假作業期末綜合復習東南大學出版社系列答案
書香天博暑假作業西安出版社系列答案
暑假作業江蘇人民出版社系列答案
新浪書業復習總動員年度總復習精要暑長江出版社系列答案
假期新觀察安徽科學技術出版社系列答案
暑假新動向電子科技大學出版社系列答案
已知函數
(1)是否存在實數
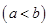 ,使得函數
,使得函數 的定義域、值域都是
的定義域、值域都是 ,若存在,則求出
,若存在,則求出 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
(2)若存在實數
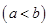 ,使得函數
,使得函數 的定義域為
的定義域為 時,值域為
時,值域為 (
(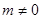 ),求
),求 的取值范圍.
的取值范圍.
把邊長為 的等邊三角形鐵皮剪去三個相同的四邊形(如圖陰影部分)后,用剩余部分做成一個無蓋的正三棱柱形容器(不計接縫),設容器的高為
的等邊三角形鐵皮剪去三個相同的四邊形(如圖陰影部分)后,用剩余部分做成一個無蓋的正三棱柱形容器(不計接縫),設容器的高為 ,容積為
,容積為 .
.
(Ⅰ)寫出函數 的解析式,并求出函數的定義域;
的解析式,并求出函數的定義域;
(Ⅱ)求當x為多少時,容器的容積最大?并求出最大容積. 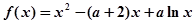 ,其中常數
,其中常數 。
。
(1)當 時,求函數
時,求函數 的單調遞增區間;
的單調遞增區間;
(2)當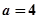 時,是否存在實數
時,是否存在實數 ,使得直線
,使得直線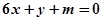 恰為曲線
恰為曲線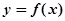 的切線?若存在,求出
的切線?若存在,求出 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(3)設定義在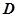 上的函數
上的函數 的圖象在點
的圖象在點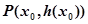 處的切線方程為
處的切線方程為 ,當
,當 時,若
時,若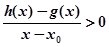 在
在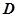 內恒成立,則稱
內恒成立,則稱 為函數
為函數 的“類對稱點”。當
的“類對稱點”。當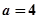 ,試問
,試問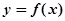 是否存在“類對稱點”?若存在,請至少求出一個“類對稱點”的橫坐標;若不存在,說明理由.
是否存在“類對稱點”?若存在,請至少求出一個“類對稱點”的橫坐標;若不存在,說明理由.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號