
 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:解答題
若定義在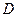 上的函數
上的函數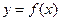
 滿足條件:存在實數
滿足條件:存在實數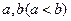 且
且

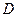 ,使得:
,使得:
⑴ 任取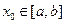 ,有
,有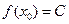 (
(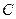 是常數);
是常數);
⑵ 對于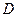 內任意
內任意 ,當
,當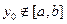 ,總有
,總有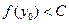 。
。
我們將滿足上述兩條件的函數 稱為“平頂型”函數,稱
稱為“平頂型”函數,稱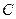 為“平頂高度”,稱
為“平頂高度”,稱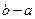 為“平頂寬度”。根據上述定義,解決下列問題:
為“平頂寬度”。根據上述定義,解決下列問題:
(1)函數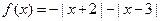 是否為“平頂型”函
是否為“平頂型”函 數?若是,求出“平頂高度”和“平頂寬度”;若不是,簡要說明理由。
數?若是,求出“平頂高度”和“平頂寬度”;若不是,簡要說明理由。
(2) 已知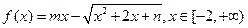 是“平頂型”函數,求出
是“平頂型”函數,求出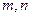 的值。
的值。
(3)對于(2)中的函數 ,若
,若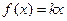 在
在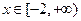 上有兩個不相等的根,求實數
上有兩個不相等的根,求實數 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數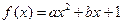 (
(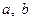 為實數,
為實數,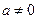 ,
,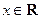 ),
),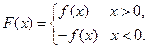
(1)若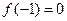 ,且函數
,且函數 的值域為
的值域為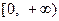 ,求
,求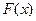 的表達式;
的表達式;
(2)在(1)的條件下,當 時,
時,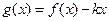 是單調函數,求實數
是單調函數,求實數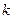 的取值范圍;
的取值范圍;
(3)設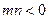 ,
,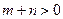 ,
,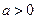 ,且函數
,且函數 為偶函數,判斷
為偶函數,判斷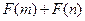 是否大于
是否大于 ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
已知函數 (
(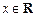 ),
),
(1)求函數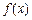 的最小值;
的最小值;
(2)已知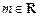 ,命題p:關于x的不等式
,命題p:關于x的不等式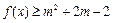 對任意
對任意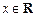 恒成立;命題q:不等式
恒成立;命題q:不等式 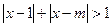 對任意
對任意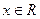 恒成立.若“p或q”為真,“p且q”為假,求實數m的取值范圍.
恒成立.若“p或q”為真,“p且q”為假,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)二次函數f(x)滿足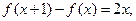 且f(0)=1.
且f(0)=1.
(1)求f(x)的解析式;
(2)在區間 上,y= f(x)的圖象恒在y=2x+m的圖象上方,試確定實數m的范圍.
上,y= f(x)的圖象恒在y=2x+m的圖象上方,試確定實數m的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知二次函數f(x)=ax2+bx+c.
(1)若f(-1)=0,試判斷函數f(x)零點的個數;
(2)是否存在a,b,c∈R,使f(x)同時滿足以下條件:
①對任意x∈R,f(-1+x)=f(-1-x),且f(x)≥0;
②對任意x∈R,都有0≤f(x)-x≤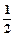 (x-1)2.若存在,求出a,b,c的值;若不存在,請說
(x-1)2.若存在,求出a,b,c的值;若不存在,請說
明理由。
(3)若對任意x1、x2∈R且x1<x2,f(x1)≠f(x2),試證明:存在x0∈(x1,x2),使f(x0)=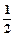 [f(x1)+f(x2)]成立。
[f(x1)+f(x2)]成立。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
在一個月內分批購入每張價值為20元的書桌共36臺,每批都購入x臺(x是正整數), 且每批均需付運費4元,儲存購入的書桌一個月所付的保管費與每批購入書桌的總價值(不含運費)成正比,若每批購入4臺,則該月需用去運費和保管費共52元,現在全月只有48元資金可以用于支付運費和保管費.
且每批均需付運費4元,儲存購入的書桌一個月所付的保管費與每批購入書桌的總價值(不含運費)成正比,若每批購入4臺,則該月需用去運費和保管費共52元,現在全月只有48元資金可以用于支付運費和保管費.
(1)求該月需用去的運費和保管費的總費用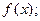
(2)能否恰當地安排每批進貨的數量,使資金夠用?寫出你的結論,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數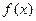 的定義域為
的定義域為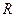 ,并滿足(1)對于一切實數
,并滿足(1)對于一切實數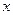 ,都有
,都有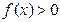 ;
;
(2)對任意的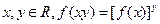 ; (3)
; (3)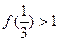 ;
;
利用以上信息求解下列問題:
(1)求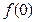 ;
;
(2)證明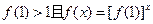 ;
;
(3)若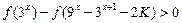 對任意的
對任意的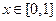 恒成立,求實數
恒成立,求實數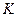 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com