
��֪���� .
.
(1)������C���c(di��n) ̎���о���
̎���о��� ����(sh��)��(sh��)
����(sh��)��(sh��) ��
�� ��ֵ��
��ֵ��
(2)�����⌍(sh��)��(sh��) ������
������ ����ֱ��
����ֱ�� :
: ���Ϸ�����(sh��)��(sh��)
���Ϸ�����(sh��)��(sh��) ��ȡֵ����.
��ȡֵ����.
(1)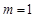 ��
�� ��(2)
��(2)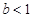 ��
��
����ԇ�}������(1)����(j��)��(d��o)��(sh��)�����x������
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)f(x)=-x3+ax2-4(
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)
��Ŀ�����Д�(sh��)�W(xu��)
��Դ��
�}�ͣ�����}
��֪����(sh��)
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б� ����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��) .��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/5f/5/1xuqs3.png" style="vertical-align:middle;" />������
.��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/5f/5/1xuqs3.png" style="vertical-align:middle;" />������ .��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/a8/2/fx31n1.png" style="vertical-align:middle;" />�^�c(di��n)
.��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/a8/2/fx31n1.png" style="vertical-align:middle;" />�^�c(di��n) ������
������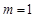 ��(2)���}��ã�����ʽ
��(2)���}��ã�����ʽ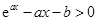 ���������������}һ���D(zhu��n)������ֵ���}.һ�Ƿ��ӑՓ��(sh��)
���������������}һ���D(zhu��n)������ֵ���}.һ�Ƿ��ӑՓ��(sh��)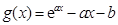 ��Сֵ������׃�����x��
��Сֵ������׃�����x��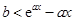 ���������(sh��)
���������(sh��)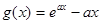 ��Сֵ.�ɷN��������
��Сֵ.�ɷN��������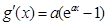 ��Ȼ��(sh��)��(sh��)a�M(j��n)��ӑՓ����(d��ng)
��Ȼ��(sh��)��(sh��)a�M(j��n)��ӑՓ����(d��ng)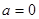 �r(sh��)��
�r(sh��)��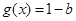 ������
������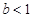 .��(d��ng)
.��(d��ng)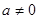 �r(sh��),��
�r(sh��),��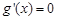 ��
�� ����Փ
����Փ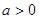 ߀��
߀��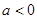 ��
��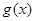 �����Ȝp��������
�����Ȝp��������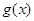 ����Сֵ��
����Сֵ��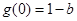 ������
������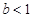 .
.
ԇ�}��������
��1��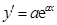 �� 2��
�� 2��
��?y��n)�����C���c(di��n)��0��1��̎���о���L�� ��
��
����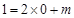 ��
��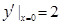 . 4��
. 4��
���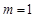 ��
�� -5��
-5��
��2����1��
�������⌍(sh��)��(sh��)a������C����ֱ����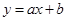 ���Ϸ����ȃr(ji��)��
���Ϸ����ȃr(ji��)��
?x,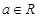 ������
������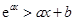 ��
��
��?x,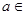 R��
R��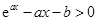 ������� 6��
������� 6��
��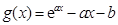 �� 7��
�� 7��
����a=0���t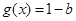 ��
��
���Ԍ�(sh��)��(sh��)b��ȡֵ������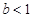 �� 8��
�� 8��
����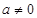 ,
,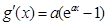 ��
��
��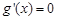 ��
�� �� 9��
�� 9��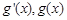 ����r���£�
����r���£�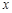
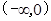
0 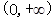
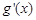
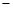
0 + 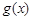


�۽�С���_��48��ϵ�д�
�۽����п�ϵ�д�
��������Q���п�ϵ�д�
�^������ϵ�д�
�_�Ľ̳�ϵ�д�
�_��15�쾫�ʺ�����Ӌ(j��)�����K�P�˿ƌW(xu��)���g(sh��)������ϵ�д�
�����óɿ�ϵ�д�
���ܴ�����ϵ�д�
��ǰһ��ϵ�д�
����ͨ����ȫ�̏�(f��)��(x��)��(d��o)��ϵ�д�

�꼉(j��)
�����n��
�꼉(j��)
�����n��
��һ
��һ���M(f��i)�n�����]��
��һ
��һ���M(f��i)�n�����]��
�߶�
�߶����M(f��i)�n�����]��
����
�������M(f��i)�n�����]��
����
�������M(f��i)�n�����]��
����
�������M(f��i)�n�����]��
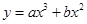 ����(d��ng)
����(d��ng)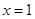 �r(sh��)���ИO��ֵ
�r(sh��)���ИO��ֵ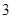 .
.
��1���� ��ֵ��
��ֵ��
��2����(sh��) �ĘOСֵ.
�ĘOСֵ. �������г���(sh��)
���������(sh��)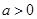 ��
��
��1����(d��ng) �r(sh��)����������
�r(sh��)���������� ̎���о����̣�
̎���о����̣�
��2�������ڌ�(sh��)��(sh��) ʹ�ò���ʽ
ʹ�ò���ʽ ��������
�������� ��ȡֵ����.
��ȡֵ����. ������m��a���錍(sh��)��(sh��)��
������m��a���錍(sh��)��(sh��)��
��1����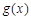 �ĘOֵ��
�ĘOֵ��
��2���O(sh��) ���������
���������
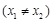 ��
�� ���������
��������� ����Сֵ��
����Сֵ��
��3���O(sh��) ��������o����
��������o���� ���څ^(q��)�g
���څ^(q��)�g �Ͽ�����
�Ͽ����� ��ʹ��
��ʹ�� ��������
�������� ��ȡֵ������
��ȡֵ������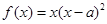 ��
��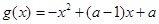 ������
������ �鳣��(sh��)����
�鳣��(sh��)����
��1���������(sh��)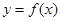 ��
��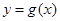 ����ͬ�ĘOֵ�c(di��n)����
����ͬ�ĘOֵ�c(di��n)���� ��ֵ��
��ֵ��
��2���O(sh��)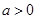 �����Ƿ����
�����Ƿ����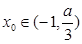 ��ʹ��
��ʹ��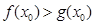 �������ڣ�Ո�����(sh��)��(sh��)
�������ڣ�Ո�����(sh��)��(sh��) ��ȡֵ�������������ڣ�Ո�f�����ɣ�
��ȡֵ�������������ڣ�Ո�f�����ɣ�
��3��ӛ����(sh��)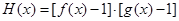 ��������(sh��)
��������(sh��)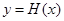 ��5��(g��)��ͬ�����c(di��n)����(sh��)��(sh��)
��5��(g��)��ͬ�����c(di��n)����(sh��)��(sh��) ��ȡֵ������
��ȡֵ������ )��
)�� ��f(x)��(d��o)����(sh��).
��f(x)��(d��o)����(sh��).
��1����(d��ng)a=2�r(sh��)���������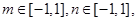 ��
�� ����Сֵ��
����Сֵ��
��2�������� ʹf(x0)>0����a��ȡֵ����.
ʹf(x0)>0����a��ȡֵ����.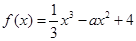 ����
���� �Ǻ���(sh��)
�Ǻ���(sh��) ��һ��(g��)�OСֵ�c(di��n).
��һ��(g��)�OСֵ�c(di��n).
��1����(sh��)��(sh��)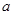 ��ֵ��
��ֵ��
��2���� �څ^(q��)�g
�څ^(q��)�g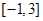 �ϵ����ֵ����Сֵ.
�ϵ����ֵ����Сֵ.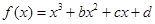 �څ^(q��)�g
�څ^(q��)�g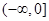 ��
��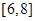 �φ��{(di��o)�f������
�φ��{(di��o)�f������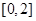 �φ��{(di��o)�f�p����D���c
�φ��{(di��o)�f�p����D���c �S����
�S���� ���c(di��n)�������c(di��n)
���c(di��n)�������c(di��n) ������(bi��o)��
������(bi��o)��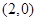 ��
��
��1����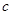 ��ֵ��
��ֵ��
��2����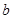 ��ȡֵ������
��ȡֵ������
��3����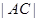 ��ȡֵ������
��ȡֵ������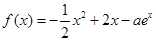 ��
��
��1����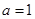 ����
����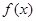 ��
��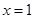 ̎���о����̣�
̎���о����̣�
��2����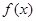 ��R����������(sh��)����(sh��)��(sh��)
��R����������(sh��)����(sh��)��(sh��)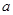 ��ȡֵ������
��ȡֵ������
���(qu��n)������վ�������£��DƬ��Դ�ھW(w��ng)�j(lu��)��������(qu��n)�����(qu��n)�wԭ�������У��D(zhu��n)�d�o���ַ����(qu��n)�������֙�(qu��n)��Ո�����ف�����֪���҂����M��̎����(li��n)ϵqq��3310059649��
ICP�䰸��̖(h��o): ��ICP��07509807̖(h��o)-10 �����W(w��ng)����42018502000812̖(h��o)