
已知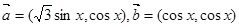 ,
,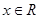 ,函數
,函數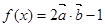 ;
;
(I)求 的最小正周期;
的最小正周期;
(II)求 在區間
在區間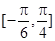 上的最大值和最小值。
上的最大值和最小值。
(I) 的最小正周期為
的最小正周期為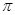 ;
;
(II)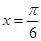 時,函數
時,函數 取得最大值2;
取得最大值2;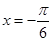 時,函數
時,函數 取得最小值
取得最小值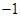 ;
;
解析試題分析:(法一)(I)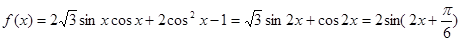 ,
,
函數 的最小正周期為
的最小正周期為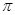 ; 4分
; 4分
(II)因為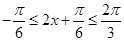 , 5分
, 5分
所以,當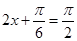 即
即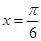 時,函數
時,函數 取得最大值2;
取得最大值2;
當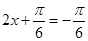 即
即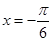 時,函數
時,函數 取得最小值
取得最小值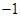 ; 9分
; 9分
(法二)(I) ,
,
函數 的最小正周期為
的最小正周期為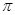 ; 4分
; 4分
(II)因為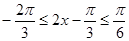 , 5分
, 5分
所以,當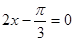 即
即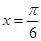 時,函數
時,函數 取得最大值2;
取得最大值2;
當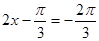 即
即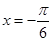 時,函數
時,函數 取得最小值
取得最小值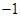 ; 9分
; 9分
考點:本題主要考查平面向量的數量積,三角函數中兩角和的正、余弦公式、二倍角公式;三角函數的周期、單調、最值等性質;考查三角函數與平面向量的綜合運用能力和化歸與轉化思想。
點評:典型題,為研究三角函數的圖象和性質,往往需要將函數“化一”,這是常考題型。本題首先通過平面向量的坐標運算,計算向量的數量積得到函數F(x)的表達式,并運用“三角公式”進行化簡,為進一步解題奠定了基礎。


科目:高中數學 來源: 題型:解答題
(本小題滿分10分)
已知向量: ,函數
,函數 ,若
,若 相鄰兩對稱軸間的距離為
相鄰兩對稱軸間的距離為
(Ⅰ)求 的值,并求
的值,并求 的最大值及相應x的集合;
的最大值及相應x的集合;
(Ⅱ)在△ABC中, 分別是A,B,C所對的邊,△ABC的面積
分別是A,B,C所對的邊,△ABC的面積 ,求邊
,求邊 的長。
的長。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com