
已知平面直角坐標系上的三點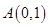 ,
,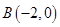 ,
, ,
, 為坐標原點,向量
為坐標原點,向量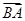 與向量
與向量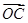 共線.
共線.
(1)求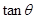 的值;
的值;
(2)求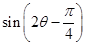 的值.
的值.
(1)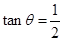 ;(2)
;(2) .
.
解析試題分析:(1)法一是利用兩平面向量共線的基本定理得到坐標之間的關系,進而利用弦化切的方法求出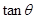 的值;法二是利用平面向量共線的基本定理結合坐標運算得到向量
的值;法二是利用平面向量共線的基本定理結合坐標運算得到向量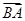 與
與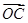 的坐標之間的關系,然后利用除法求出
的坐標之間的關系,然后利用除法求出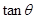 的值;(2)利用(1)中
的值;(2)利用(1)中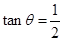 以及同角三角函數中的商數關系和平方關系并結合角
以及同角三角函數中的商數關系和平方關系并結合角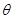 的范圍列方程組求出
的范圍列方程組求出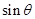 和
和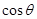 的值,進而求出
的值,進而求出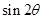 和
和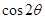 的值,最終再利用兩角差的正弦公式求出
的值,最終再利用兩角差的正弦公式求出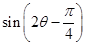 的值.
的值.
試題解析:法1:由題意得: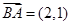 ,
,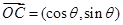 , 2分
, 2分
∵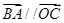 ,∴
,∴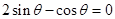 ,∴
,∴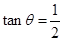 . 5分
. 5分
法2:由題意得: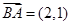 ,
,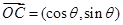 , 2分
, 2分
∵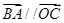 ,∴
,∴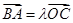 ,∴
,∴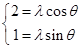 ,∴
,∴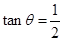 . 5分
. 5分
(2)∵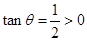 ,
,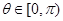 ,∴
,∴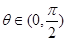 , 6分
, 6分
由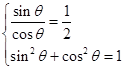 ,解得
,解得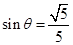 ,
, , 8分
, 8分
∴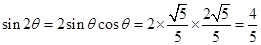 ; 9分
; 9分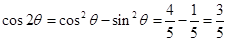 ; 10分
; 10分
∴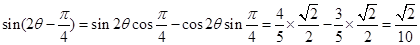 . 12分
. 12分
考點:1.平面向量的坐標運算;2.同角三角函數的基本關系;3.二倍角;4.兩角差的正弦公式


科目:高中數學 來源: 題型:解答題
如圖所示,扇形AOB,圓心角AOB的大小等于 ,半徑為2,在半徑OA上有一動點C,過點C作平行于OB的直線交弧AB于點P.
,半徑為2,在半徑OA上有一動點C,過點C作平行于OB的直線交弧AB于點P.
(1)若C是半徑OA的中點,求線段PC的長;
(2)設 ,求
,求 面積的最大值及此時
面積的最大值及此時 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com