
已知函數(shù)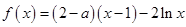 ,
,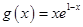 (
( ,
,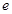 為自然對(duì)數(shù)的底數(shù)).
為自然對(duì)數(shù)的底數(shù)).
(1)當(dāng)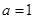 時(shí),求
時(shí),求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)對(duì)任意的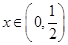 ,
,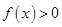 恒成立,求
恒成立,求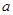 的最小值;
的最小值;
(3)若對(duì)任意給定的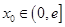 ,在
,在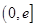 上總存在兩個(gè)不同的
上總存在兩個(gè)不同的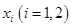 ,使得
,使得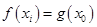 成立,求
成立,求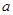 的取值范圍.
的取值范圍.
(1)函數(shù)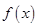 的單調(diào)減區(qū)間為
的單調(diào)減區(qū)間為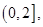 單調(diào)增區(qū)間為
單調(diào)增區(qū)間為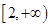 ;(2)實(shí)數(shù)
;(2)實(shí)數(shù)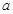 的最小值為
的最小值為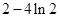 ;
;
(3)實(shí)數(shù)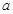 的取值范圍是
的取值范圍是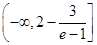 .
.
解析試題分析:(1)把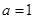 代入函數(shù)
代入函數(shù)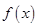 的解析式,直接利用導(dǎo)數(shù)求函數(shù)
的解析式,直接利用導(dǎo)數(shù)求函數(shù)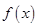 在定義域上的單調(diào)區(qū)間;(2)利用參數(shù)分離法將問(wèn)題中的不等式等價(jià)轉(zhuǎn)化為
在定義域上的單調(diào)區(qū)間;(2)利用參數(shù)分離法將問(wèn)題中的不等式等價(jià)轉(zhuǎn)化為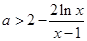 在
在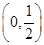 上恒成立,即
上恒成立,即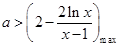 ,進(jìn)而求出參數(shù)
,進(jìn)而求出參數(shù)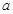 的取值范圍,從而求出
的取值范圍,從而求出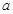 的最小值;(3)先利用導(dǎo)數(shù)求出函數(shù)
的最小值;(3)先利用導(dǎo)數(shù)求出函數(shù)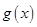 在
在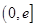 上的值域,利用導(dǎo)數(shù)研究函數(shù)
上的值域,利用導(dǎo)數(shù)研究函數(shù)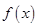 的單調(diào)性,并求出方程
的單調(diào)性,并求出方程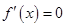 的唯一根
的唯一根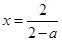 ,將條件“對(duì)于任意給定的
,將條件“對(duì)于任意給定的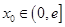 ,在
,在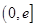 總存在兩個(gè)不同的
總存在兩個(gè)不同的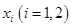 ,使得
,使得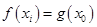 ”轉(zhuǎn)化為“函數(shù)
”轉(zhuǎn)化為“函數(shù)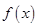 在區(qū)間
在區(qū)間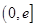 上存在唯一極值點(diǎn)
上存在唯一極值點(diǎn)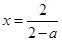 ,即
,即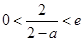 ,且函數(shù)
,且函數(shù)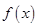 在區(qū)間
在區(qū)間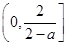 和區(qū)間
和區(qū)間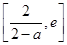 上的值域均包含函數(shù)
上的值域均包含函數(shù)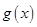 在區(qū)間
在區(qū)間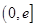 上的值域”,從而列出相應(yīng)的不等式進(jìn)行求解參數(shù)
上的值域”,從而列出相應(yīng)的不等式進(jìn)行求解參數(shù)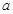 的取值范圍.
的取值范圍.
試題解析:(1)當(dāng)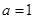 時(shí),
時(shí),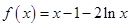 ,
,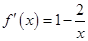 ,
,
由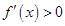 ,
,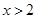 ,由
,由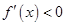 ,
,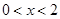 ,
,
故 的單調(diào)減區(qū)間為
的單調(diào)減區(qū)間為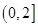 ,單調(diào)增區(qū)間為
,單調(diào)增區(qū)間為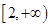 ;
;
(2)即對(duì)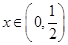 ,
,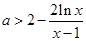 恒成立,
恒成立,
令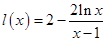 ,
,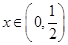 ,則
,則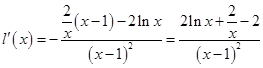 ,
,
再令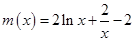 ,
,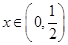 ,
,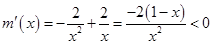 ,
,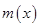 在
在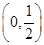 上為減函數(shù),于是
上為減函數(shù),于是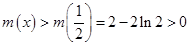 ,
,
從而,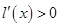 ,于是
,于是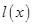 在
在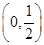 上為增函數(shù),
上為增函數(shù),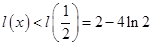 ,
,
故要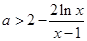 恒成立,只要
恒成立,只要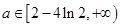 ,即
,即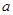 的最小值為
的最小值為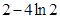 ;
;
(3)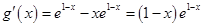 ,當(dāng)
,當(dāng)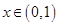 時(shí),
時(shí),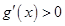 ,函數(shù)
,函數(shù)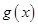 單調(diào)遞增,
單調(diào)遞增,
當(dāng)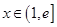 時(shí),
時(shí),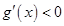 ,函數(shù)
,函數(shù)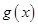 單調(diào)遞減,
單調(diào)遞減,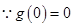 ,
,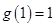 ,
,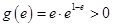 ,
,
所以,函數(shù)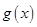 在
在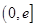 上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/cd/2/14kyl2.png" style="vertical-align:middle;" />.
上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/cd/2/14kyl2.png" style="vertical-align:middle;" />.
當(dāng)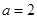 時(shí),不合題意;
時(shí),不合題意;



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)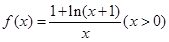
(I)函數(shù) 在區(qū)間
在區(qū)間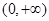 上是增函數(shù)還是減函數(shù)?證明你的結(jié)論;
上是增函數(shù)還是減函數(shù)?證明你的結(jié)論;
(II)當(dāng)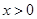 時(shí),
時(shí),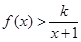 恒成立,求整數(shù)
恒成立,求整數(shù)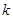 的最大值;
的最大值;
(Ⅲ)試證明: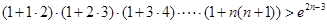
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,某自來(lái)水公司要在公路兩側(cè)排水管,公路為東西方向,在路北側(cè)沿直線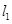 排水管,在路南側(cè)沿直線
排水管,在路南側(cè)沿直線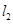 排水管(假設(shè)水管與公路的南,北側(cè)在一條直線上且水管的大小看作為一條直線),現(xiàn)要在矩形區(qū)域ABCD內(nèi)沿直線EF將
排水管(假設(shè)水管與公路的南,北側(cè)在一條直線上且水管的大小看作為一條直線),現(xiàn)要在矩形區(qū)域ABCD內(nèi)沿直線EF將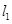 與
與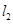 接通.已知AB = 60m,BC = 60
接通.已知AB = 60m,BC = 60 m,公路兩側(cè)排管費(fèi)用為每米1萬(wàn)元,穿過(guò)公路的EF部分的排管費(fèi)用為每米2萬(wàn)元,設(shè)EF與AB所成角為
m,公路兩側(cè)排管費(fèi)用為每米1萬(wàn)元,穿過(guò)公路的EF部分的排管費(fèi)用為每米2萬(wàn)元,設(shè)EF與AB所成角為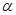 .矩形區(qū)域內(nèi)的排管費(fèi)用為W.
.矩形區(qū)域內(nèi)的排管費(fèi)用為W.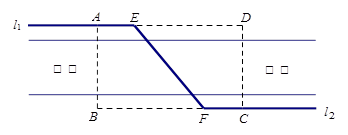
(1)求W關(guān)于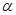 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)求W的最小值及相應(yīng)的角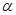 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù)h(x)=ax2+bx+c(其中c<3),其導(dǎo)函數(shù)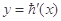 的圖象如圖,f(x)=6lnx+h(x)
的圖象如圖,f(x)=6lnx+h(x)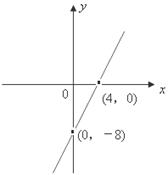
(1)求f(x)在x=3處的切線斜率;
(2)若f(x)在區(qū)間(m,m+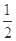 )上是單調(diào)函數(shù),求實(shí)數(shù)m的取值范圍;
)上是單調(diào)函數(shù),求實(shí)數(shù)m的取值范圍;
(3)若對(duì)任意k∈[-1,1],函數(shù)y=kx(x∈(0,6])的圖象總在函數(shù)y=f(x)圖象的上方,求c的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)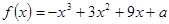 .
.
(1)求 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(2)若 在區(qū)間
在區(qū)間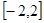 上的最大值為
上的最大值為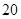 ,求它在該區(qū)間上的最小值.
,求它在該區(qū)間上的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知x=1是函數(shù)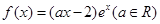 的一個(gè)極值點(diǎn),
的一個(gè)極值點(diǎn),
(Ⅰ)求a的值;
(Ⅱ)當(dāng)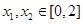 時(shí),證明:
時(shí),證明: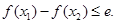
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)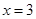 是函數(shù)
是函數(shù)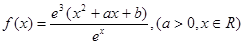 的一個(gè)極值點(diǎn).
的一個(gè)極值點(diǎn).
(1)求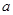 與
與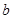 的關(guān)系式(用
的關(guān)系式(用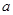 表示
表示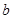 ),并求
),并求 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)設(shè)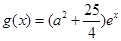 ,若存在
,若存在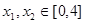 使得
使得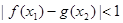 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)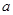 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)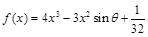 ,其中
,其中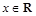 ,
,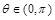 .
.
(Ⅰ)若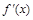 的最小值為
的最小值為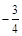 ,試判斷函數(shù)
,試判斷函數(shù) 的零點(diǎn)個(gè)數(shù),并說(shuō)明理由;
的零點(diǎn)個(gè)數(shù),并說(shuō)明理由;
(Ⅱ)若函數(shù) 的極小值大于零,求
的極小值大于零,求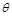 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com