
題目列表(包括答案和解析)
21.(本小題滿分14分)設函數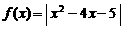 .
.
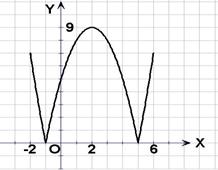
(Ⅰ)在區間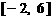 上畫出函數
上畫出函數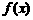 的圖像;
的圖像;
(Ⅱ)設集合 . 試判斷集合
. 試判斷集合 和
和 之間的關系,并給出證明;
之間的關系,并給出證明;
(Ⅲ)當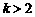 時,求證:在區間
時,求證:在區間 上,
上,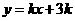 的圖像位于函數
的圖像位于函數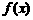 圖像的上方
圖像的上方
解:(Ⅰ)
(Ⅱ)方程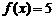 的解分別是
的解分別是 和
和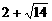 ,由于
,由于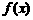 在
在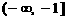 和
和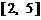 上單調遞減,在
上單調遞減,在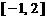 和
和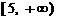 上單調遞增,因此
上單調遞增,因此
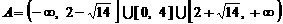 .
.
由于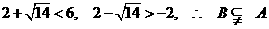 .
.
(Ⅲ)[解法一] 當 時,
時, .
.
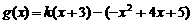
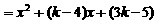
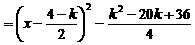 ,
,
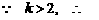
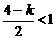 . 又
. 又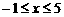 ,
,
①
當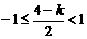 ,即
,即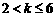 時,取
時,取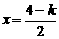 ,
,

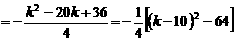 .
.
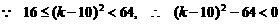 ,
,
則 .
.
②
當 ,即
,即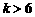 時,取
時,取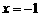 ,
,  =
=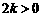 .
.
由 ①、②可知,當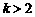 時,
時,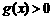 ,
, .
.
因此,在區間 上,
上,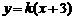 的圖像位于函數
的圖像位于函數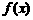 圖像的上方.
圖像的上方.
[解法二] 當 時,
時, .
.
由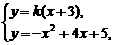 得
得 ,
,
令 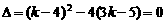 ,解得
,解得 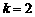 或
或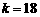 ,
,
在區間 上,當
上,當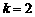 時,
時,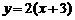 的圖像與函數
的圖像與函數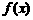 的圖像只交于一點
的圖像只交于一點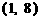 ;
;
當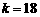 時,
時, 的圖像與函數
的圖像與函數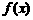 的圖像沒有交點.
的圖像沒有交點.
如圖可知,由于直線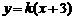 過點
過點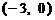 ,當
,當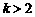 時,直線
時,直線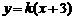 是由直線
是由直線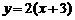 繞點
繞點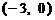 逆時針方向旋轉得到. 因此,在區間
逆時針方向旋轉得到. 因此,在區間 上,
上,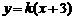 的圖像位于函數
的圖像位于函數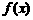 圖像的上方.
圖像的上方.
20.(本小題滿分14分)已知:定義在R上的函數f (x)為奇函數,且在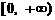 上是增函數.
上是增函數.
(Ⅰ)求證:f (x)在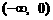 上也是增函數;
上也是增函數;
(Ⅱ)對任意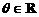 ,求實數m的取值范圍,使不等式
,求實數m的取值范圍,使不等式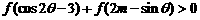 恒成立.
恒成立.
解:(Ⅰ)證明:設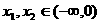 ,且
,且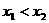 ,
,
則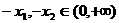 ,且
,且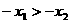 .
.
∵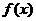 在
在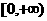 上是增函數,∴
上是增函數,∴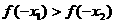 .
.
又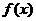 為奇函數,∴
為奇函數,∴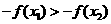 ,
,
∴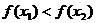 , 即
, 即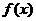 在
在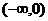 上也是增函數.
上也是增函數.
(Ⅱ)∵函數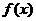 在
在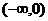 和
和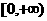 上是增函數,且
上是增函數,且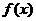 在R上是奇函數,
在R上是奇函數,
∴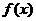 在
在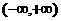 上是增函數.
上是增函數.
于是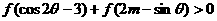





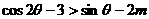

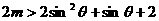

 .
.
∵當 時,
時,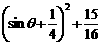 的最大值為
的最大值為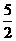 ,∴當
,∴當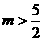 時,不等式恒成立.
時,不等式恒成立.
19.(本小題滿分14分)設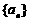 為公差大于0的等差數列,
為公差大于0的等差數列,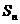 為數列
為數列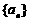 的前n項的和.
的前n項的和.
已知S4=24,
(Ⅰ)求數列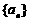 的通項公式
的通項公式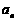 ;
;
(Ⅱ)若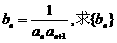 的前n項和
的前n項和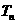
解:(Ⅰ)
由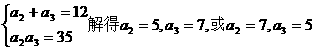
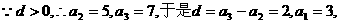
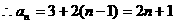
(Ⅱ)
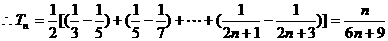
18.(本小題滿分16分)已知函數 .
.
(Ⅰ)求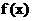 的最小正周期及遞減區間;
的最小正周期及遞減區間;
(Ⅱ)指出將函數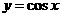 的圖象經過怎樣的變換而得到函數
的圖象經過怎樣的變換而得到函數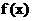 的圖象;
的圖象;
(Ⅲ)若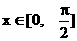 , 求
, 求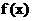 最大值、最小值.
最大值、最小值.
解:(Ⅰ)
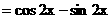
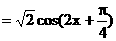 ∴
∴ 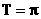
遞減區間
(Ⅱ)先把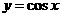 各點的橫坐標縮小到原來的
各點的橫坐標縮小到原來的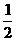 (縱坐標不變),再向左平移
(縱坐標不變),再向左平移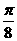 個單位,再把縱坐標擴大到原來的
個單位,再把縱坐標擴大到原來的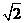 倍(橫坐標不變)而得到函數
倍(橫坐標不變)而得到函數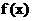 的圖象
的圖象
(Ⅲ)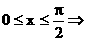
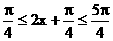
當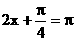 即
即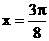 時
時 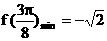
當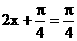 即
即 時
時 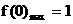
17.(本小題滿分12分)有四個正數 ,前三數成等比數列,其和為
,前三數成等比數列,其和為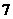 ;后三數成等差數列,其和為
;后三數成等差數列,其和為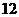 .
.
(Ⅰ)求此四數;
(Ⅱ)分別求以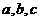 為前三項的等比數列的前
為前三項的等比數列的前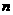 項和
項和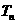 與以
與以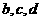 為前三項的等差數列的
為前三項的等差數列的
前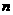 項和
項和 ;
;
(Ⅲ)比較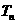 與
與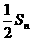 的大小.
的大小.
解:(Ⅰ)依題意有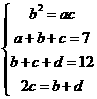
解得四數依次為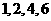 或
或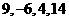 ,因為四數均為正數。所以所求四數依次為
,因為四數均為正數。所以所求四數依次為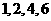
(Ⅱ)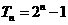 ,
,
(Ⅲ)當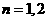 時,
時,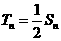
當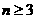 時,
時,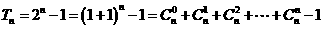

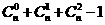
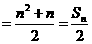
16.給出下列四個函數:①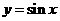 ;②
;②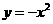 ;③
;③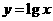 ;④
;④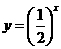 ,對于其定義域內的任意的
,對于其定義域內的任意的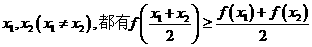 成立的函數為 ②③
成立的函數為 ②③
15.定義運算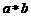 為:
為: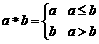 ,例如,
,例如,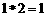 ,則函數
,則函數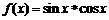 的值域[-1,
的值域[-1,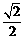 ]
]
14.已知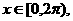 且
且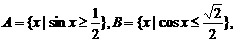 則A∩B=
則A∩B= 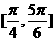
13.已知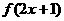 是偶函數,則函數
是偶函數,則函數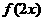 的圖象的對稱軸是
的圖象的對稱軸是 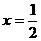
12.一條信息,若一人得知后,一小時內將信息傳給兩人,這兩人又在一小時內各傳給未知信息的另外兩人.如此下去,要傳遍55人的班級所需時間大約為__5_____小時.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com