
設(shè)函數(shù)f(x)="|2x-1|+|2x-3|" , x∈R.
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若 的定義域?yàn)镽,求實(shí)數(shù)m的取值范圍.
的定義域?yàn)镽,求實(shí)數(shù)m的取值范圍.
(Ⅰ) {x∣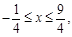 }. (Ⅱ) m >-2 。
}. (Ⅱ) m >-2 。
解析試題分析:(Ⅰ)∵ f(x)="|2x-1|+|2x-3|" , f(x)≤5
∴有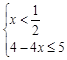 或
或 或
或
解得: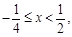 或
或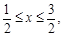 或
或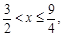
∴不等式的解集為:{x∣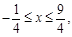 }. 5分
}. 5分
(Ⅱ) 若 的定義域?yàn)镽,則f(x)+m≠0恒成立,
的定義域?yàn)镽,則f(x)+m≠0恒成立,
即f(x)+m=0在R上無(wú)解.
又f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2,
∴f(x)最小值為2,
∴m >-2 10分
考點(diǎn):本題主要考查絕對(duì)值不等式的解法,絕對(duì)值不等式恒成立問(wèn)題。
點(diǎn)評(píng):中檔題,絕對(duì)值不等式的解法,應(yīng)立足于“去絕對(duì)值符號(hào)”,一種思路是利用定義分類(lèi)討論,一種思路是通過(guò)平方,另一種思路是不去絕對(duì)值符號(hào),利用幾何意義。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù) 是冪函數(shù)且在
是冪函數(shù)且在 上為減函數(shù),函數(shù)
上為減函數(shù),函數(shù) 在區(qū)間
在區(qū)間 上的最大值為2,試求實(shí)數(shù)
上的最大值為2,試求實(shí)數(shù) 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(1)已知函數(shù)y=ln(-x2+x-a)的定義域?yàn)椋ǎ?,3),求實(shí)數(shù)a的取值范圍;
(2)已知函數(shù)y=ln(-x2+x-a)在(-2,3)上有意義,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知y=f(x)是定義在R上的奇函數(shù),當(dāng)x≤0時(shí),f(x)=2x+x2.
(1)求x>0時(shí),f(x)的解析式;
(2)若關(guān)于x的方程f(x)=2a2+a有三個(gè)不同的解,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知f(x)的定義域?yàn)?0,+∞),且滿足f(2)=1,f(xy)=f(x)+f(y),又當(dāng)x2>x1>0時(shí),f(x2)>f(x1).
(1)求f(1)、f(4)、f(8)的值;
(2)若有f(x)+f(x-2)≤3成立,求x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知曲線  在點(diǎn)
在點(diǎn)  處的切線
處的切線  平行直線
平行直線 ,且點(diǎn)
,且點(diǎn) 在第三象限.
在第三象限.
(Ⅰ)求 的坐標(biāo);
的坐標(biāo);
(Ⅱ)若直線 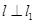 , 且
, 且  也過(guò)切點(diǎn)
也過(guò)切點(diǎn) ,求直線
,求直線 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知 ,
,
(1)討論 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若對(duì)任意的 ,且
,且 ,有
,有 ,求實(shí)數(shù)
,求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù) 在
在 與
與 時(shí)都取得極值
時(shí)都取得極值
(1)求 的值與函數(shù)
的值與函數(shù) 的單調(diào)區(qū)間
的單調(diào)區(qū)間
(2)若對(duì) ,不等式
,不等式 恒成立,求
恒成立,求 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)f(x)=1n(2ax+1)+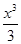 -x2-2ax(a∈R).
-x2-2ax(a∈R).
(1)若y=f(x)在[4,+∞)上為增函數(shù),求實(shí)數(shù)a的取值范圍;
(2)當(dāng)a= 時(shí),方程f(1-x)=
時(shí),方程f(1-x)=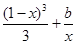 有實(shí)根,求實(shí)數(shù)b的最大值.
有實(shí)根,求實(shí)數(shù)b的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com