
已知函數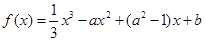 (
(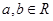 ),其圖像在點(1,
),其圖像在點(1,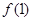 )處的切線方程為
)處的切線方程為 .
.
(1)求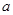 ,
,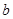 的值;
的值;
(2)求函數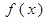 的單調區間和極值;
的單調區間和極值;
(3)求函數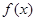 在區間[-2,5]上的最大值.
在區間[-2,5]上的最大值.
(1) 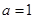 ,
,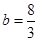 .
.
(2)函數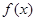 的極大值是
的極大值是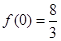 ,極小值是
,極小值是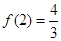 .
.
(3)函數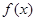 在區間
在區間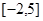 上的最大值為
上的最大值為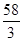 .
.
解析試題分析:(1) 由題意,
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
設函數
科目:高中數學
來源:
題型:解答題
已知函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 . 1分
. 1分
又∵函數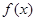 的圖象在點
的圖象在點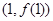 處的切線方程為
處的切線方程為 ,
,
所以切線的斜率為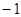 ,
,
即 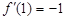 ,∴
,∴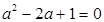 ,解得
,解得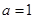 . 2分
. 2分
又∵點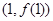 在直線
在直線 上,∴
上,∴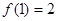 , 3分
, 3分
同時點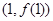 即點
即點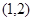 在
在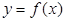 上,
上,
∴ , 4分
, 4分
即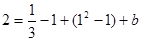 ,解得
,解得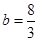 . 5分
. 5分
(2)由(1)有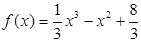 ,
,
∴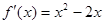 , 6分
, 6分
由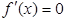 可知
可知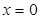 ,或
,或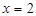 ,所以有
,所以有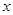 、
、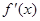 、
、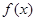 的變化情況表如下:
的變化情況表如下: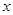
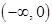
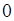
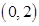
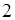
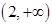
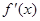
+ 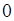
- 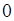
+ 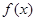
極大值 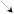


燦爛在六月模擬強化測試精編系列答案
測試卷全新升級版系列答案
測試新方案系列答案
常德標準卷系列答案
超級奧賽培優競賽系列答案
超級考卷系列答案
超級培優系列答案
超級英語系列答案
晨光全優同步指導訓練與檢測系列答案
成功寶典系列答案
 ,
,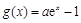 (其中
(其中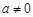 ,
,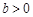 ),且函數
),且函數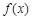 的圖象在點
的圖象在點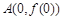 處的切線與函數
處的切線與函數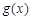 的圖象在點
的圖象在點 處的切線重合.
處的切線重合.
(Ⅰ)求實數a,b的值;
(Ⅱ)若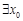 ,滿足
,滿足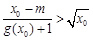 ,求實數
,求實數 的取值范圍;
的取值范圍;
(Ⅲ)若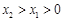 ,試探究
,試探究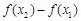 與
與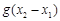 的大小,并說明你的理由.
的大小,并說明你的理由. .
.
(1)若 ,試求函數
,試求函數 的單調區間;
的單調區間;
(2)過坐標原點 作曲線
作曲線 的切線,證明:切點的橫坐標為1;
的切線,證明:切點的橫坐標為1;
(3)令 ,若函數
,若函數 在區間(0,1]上是減函數,求
在區間(0,1]上是減函數,求 的取值范圍.
的取值范圍.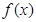 的導數
的導數 為實數,
為實數, .
.
(Ⅰ)若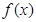 在區間[-1,1]上的最小值、最大值分別為-2、1,求a、b的值;
在區間[-1,1]上的最小值、最大值分別為-2、1,求a、b的值;
(Ⅱ)在(Ⅰ)的條件下,求經過點 且與曲線
且與曲線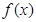 相切的直線
相切的直線 的方程;
的方程;
(Ⅲ)設函數 ,試判斷函數
,試判斷函數 的極值點個數。
的極值點個數。
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號