
已知冪函數 的圖象與x軸,y軸無交點且關于原點對稱,又有函數f(x)=x2-alnx+m-2在(1,2]上是增函數,g(x)=x-
的圖象與x軸,y軸無交點且關于原點對稱,又有函數f(x)=x2-alnx+m-2在(1,2]上是增函數,g(x)=x- 在(0,1)上為減函數.
在(0,1)上為減函數.
①求a的值;
②若 ,數列{an}滿足a1=1,an+1=p(an),(n∈N+),數列{bn},滿足
,數列{an}滿足a1=1,an+1=p(an),(n∈N+),數列{bn},滿足 ,
, ,求數列{an}的通項公式an和sn.
,求數列{an}的通項公式an和sn.
③設 ,試比較[h(x)]n+2與h(xn)+2n的大小(n∈N+),并說明理由.
,試比較[h(x)]n+2與h(xn)+2n的大小(n∈N+),并說明理由.
① ;②
;② ;
; ;③見解析.
;③見解析.
解析試題分析:①由冪函數的定義和性質可以知道 的取值集合,由圖像關于原點對稱的函數是奇函數可以確定
的取值集合,由圖像關于原點對稱的函數是奇函數可以確定 的值,將
的值,將 的值代入
的值代入 ,
, 的解析式后,根據函數的單調性與導函數的關系以及不等式的恒成立問題的解法就可以知道
的解析式后,根據函數的單調性與導函數的關系以及不等式的恒成立問題的解法就可以知道 滿足的不等式,就可以解得
滿足的不等式,就可以解得 的值;②先由已知條件求出
的值;②先由已知條件求出 的解析式,然后得出
的解析式,然后得出 ,
, 的關系,由函數構造的方法可以求得
的關系,由函數構造的方法可以求得 的解析式,代入
的解析式,代入 即可,再由數列求和公式求得
即可,再由數列求和公式求得 的值;③先求出
的值;③先求出 的解析式,再由相減的方法來判斷兩個式子的大小,最后減得的結果和0比較即可,注意分類討論的思想.
的解析式,再由相減的方法來判斷兩個式子的大小,最后減得的結果和0比較即可,注意分類討論的思想.
試題解析:①冪函數的圖像與 軸,
軸, 軸無交點,則有
軸無交點,則有 ,解得
,解得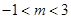
又 ,∴
,∴ 或
或 ,
,
又冪函數的圖像關于原點對稱,則有冪函數是奇函數,
當 時,
時, 是偶函數,不合題意,舍去,
是偶函數,不合題意,舍去,
當 時,
時, 是奇函數,∴
是奇函數,∴ ,
,
∴ ,求導得
,求導得 ,
,
又∵ 在
在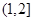 上是增函數,∴
上是增函數,∴ 在
在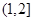 上恒成立,
上恒成立,
解得 ,
,
又∵ ,
, 在
在 上為減函數,
上為減函數,
∴ 在
在 上恒成立,
上恒成立,
解得 ,
,
綜上知 ; ..3分
; ..3分
②∵ ,
,
∴ ∴
∴ ∴
∴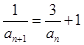 ∴
∴ ,
,
∴ 是首項為
是首項為 公比
公比 的等比數列,
的等比數列,
∴ 解得
解得 ,
,
∴ ,
,
∴ ,
, ; .6分
; .6分
③∵ ,
,
當 時,
時, ,
,
當 時,
時,
=
=
=
=
 ,
, . 10分
. 10分
考點:函數的單調性與導函數的關系,奇函數圖像的性質,等比數列的構造.


科目:高中數學 來源: 題型:解答題
某地開發了一個旅游景點,第1年的游客約為100萬人,第2年的游客約為120萬人.某數學興趣小組綜合各種因素預測:①該景點每年的游客人數會逐年增加;②該景點每年的游客都達不到130萬人.該興趣小組想找一個函數 來擬合該景點對外開放的第
來擬合該景點對外開放的第
 年與當年的游客人數
年與當年的游客人數 (單位:萬人)之間的關系.
(單位:萬人)之間的關系.
(1)根據上述兩點預測,請用數學語言描述函數 所具有的性質;
所具有的性質;
(2)若 =
= ,試確定
,試確定 的值,并考察該函數是否符合上述兩點預測;
的值,并考察該函數是否符合上述兩點預測;
(3)若 =
= ,欲使得該函數符合上述兩點預測,試確定
,欲使得該函數符合上述兩點預測,試確定 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,
, 
 .
.
(1)若 , 函數
, 函數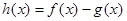 在其定義域是增函數,求
在其定義域是增函數,求 的取值范圍;
的取值范圍;
(2)在(1)的結論下,設函數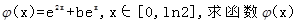 的最小值;
的最小值;
(3)設函數 的圖象
的圖象 與函數
與函數 的圖象
的圖象 交于點
交于點 ,過線段
,過線段 的中點
的中點 作
作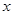 軸的垂線分別交
軸的垂線分別交 、
、 于點
于點 、
、 ,問是否存在點
,問是否存在點 ,使
,使 在
在 處的切線與
處的切線與 在
在 處的切線平行?若存在,求出
處的切線平行?若存在,求出 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 ,若在定義域內存在實數
,若在定義域內存在實數 ,滿足
,滿足 ,則稱
,則稱 為“局部奇函數”.
為“局部奇函數”.
(Ⅰ)已知二次函數 ,試判斷
,試判斷 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(Ⅱ)若 是定義在區間
是定義在區間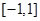 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數 的取值范圍;
的取值范圍;
(Ⅲ)若 為定義域
為定義域 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 .
.
(1)若x= 時,
時, 取得極值,求
取得極值,求 的值;
的值;
(2)若 在其定義域內為增函數,求
在其定義域內為增函數,求 的取值范圍;
的取值范圍;
(3)設 ,當
,當 =-1時,證明
=-1時,證明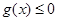 在其定義域內恒成立,并證明
在其定義域內恒成立,并證明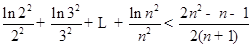 (
( ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 的定義域為
的定義域為 ,若
,若 在
在 上為增函數,則稱
上為增函數,則稱 為“一階比增函數”.
為“一階比增函數”.
(Ⅰ) 若 是“一階比增函數”,求實數
是“一階比增函數”,求實數 的取值范圍;
的取值范圍;
(Ⅱ) 若 是“一階比增函數”,求證:
是“一階比增函數”,求證: ,
, ;
;
(Ⅲ)若 是“一階比增函數”,且
是“一階比增函數”,且 有零點,求證:
有零點,求證: 有解.
有解.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com