
已知直角 的三邊長
的三邊長 ,滿足
,滿足
(1)在 之間插入2011個數,使這2013個數構成以
之間插入2011個數,使這2013個數構成以 為首項的等差數列
為首項的等差數列 ,且它們的和為
,且它們的和為 ,求的最小值;
,求的最小值;
(2)已知 均為正整數,且
均為正整數,且 成等差數列,將滿足條件的三角形的面積從小到大排成一列
成等差數列,將滿足條件的三角形的面積從小到大排成一列 ,且
,且 ,求滿足不等式
,求滿足不等式 的所有
的所有 的值;
的值;
(3)已知 成等比數列,若數列
成等比數列,若數列 滿足
滿足 ,證明:數列
,證明:數列 中的任意連續三項為邊長均可以構成直角三角形,且
中的任意連續三項為邊長均可以構成直角三角形,且 是正整數.
是正整數.
(1)最小值為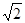 ; (2) 2、3、4.
; (2) 2、3、4.
(3)證明:由 成等比數列,
成等比數列, .
.
由于 為直角三角形的三邊長,證明數列
為直角三角形的三邊長,證明數列 中的任意連續三項為邊長均可以構成直角三角形. 證得
中的任意連續三項為邊長均可以構成直角三角形. 證得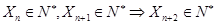 ,
,
故對于任意的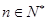 都有
都有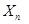 是正整數.
是正整數.
解析試題分析:(1) 是等差數列,∴
是等差數列,∴ ,即
,即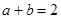 . 2分
. 2分
所以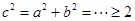 ,的最小值為
,的最小值為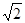 ; 4分
; 4分
(2) 設 的公差為
的公差為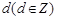 ,則
,則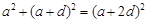
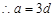 5分
5分
設三角形的三邊長為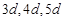 ,面積
,面積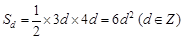 ,
,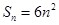 ,
,
 . 7分
. 7分
由 得
得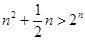 ,
,
當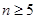 時,
時,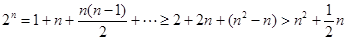 ,
,
經檢驗當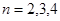 時,
時,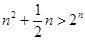 ,當
,當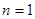 時,
時,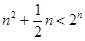 9分
9分
綜上所述,滿足不等式 的所有
的所有 的值為2、3、4. 10分
的值為2、3、4. 10分
(3)證明:因為 成等比數列,
成等比數列, .
.
由于 為直角三角形的三邊長,知
為直角三角形的三邊長,知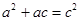 ,
,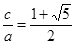 , 11分
, 11分
又 ,得
,得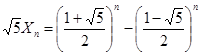 ,
,
于是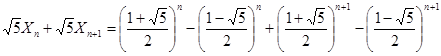
 .… 12分
.… 12分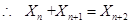 ,則有
,則有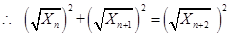 .
.
故數列 中的任意連續三項為邊長均可以構成直角三角形. 14分
中的任意連續三項為邊長均可以構成直角三角形. 14分
因為 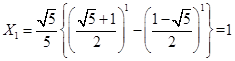 ,
,
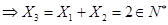 , 15分
, 15分
由 ,同理可得
,同理可得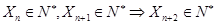 ,
,
故對于任意的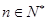 都有
都有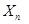 是正整數. 16分
是正整數. 16分
考點:本題主要考查等差數列、等比數列的基礎知識,構成直角三角形的條件。
點評:難題,本題綜合性較強,涉及等差數列、等比數列、不等式及構成直角三角形的條件。對法則是自點變形能力要求高,易出錯。


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com