
題目列表(包括答案和解析)
7、若以連續擲兩次骰子分別得到的點數 、
、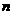 作為點P的橫、縱坐標,則點P在直線
作為點P的橫、縱坐標,則點P在直線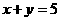 下方的概率是( )
下方的概率是( )
A、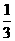 B、
B、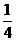 C、
C、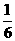 D、
D、
6、已知直線 、
、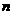 及平面
及平面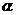 ,下列命題中的真命題是( )
,下列命題中的真命題是( )
A、若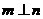 ,
,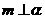 ,則
,則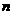 ∥
∥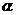 B、若
B、若 ∥
∥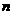 ,
,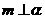 ,則
,則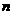 ∥
∥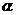
C、若 ∥
∥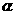 ,
,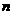 ∥
∥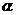 ,則
,則 ∥
∥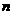 D、若
D、若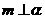 ,
,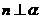 ,則
,則 ∥
∥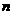
5、已知函數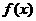 、
、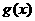 定義在R上,
定義在R上,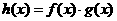 ,則“
,則“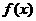 、
、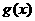 均為奇函數”是“
均為奇函數”是“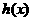 為偶函數”的(
)
為偶函數”的(
)
A、充分不必要條件 B、必要不充分條件
C、充要條件 D、既不充分也不必要條件
4、將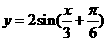 的圖象按向量
的圖象按向量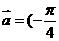 ,
,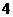 )平移,則平移后所得圖象的解析式為( )
)平移,則平移后所得圖象的解析式為( )
A、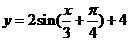 B、
B、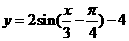
C、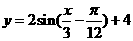 D、
D、
3、函數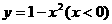 的反函數為 ( )
的反函數為 ( )
A、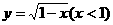 B、
B、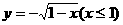
C、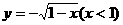 D、
D、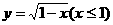
2、已知等差數列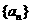 中,
中,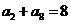 ,則該數列前9項和
,則該數列前9項和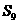 等于 ( )
等于 ( )
A、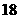 B、
B、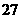 C、
C、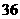 D、
D、
1、已知集合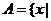
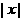 ≤
≤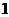
 ,
,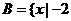 ≤
≤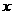 <
<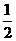
 ,則
,則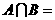 ( )
( )
A、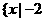 ≤
≤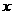 ≤
≤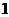
 B、
B、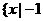 ≤
≤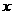 <
<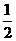

C、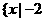 ≤
≤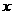 <
<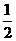
 D、
D、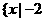 ≤
≤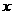 <
<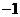

22.(本小題滿分1 4分)
已知函數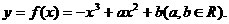
(Ⅰ)要使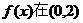 上單調遞增,試求a的取值范圍;
上單調遞增,試求a的取值范圍;
(Ⅱ)當a<0時,若函數滿足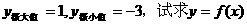 的解析式;
的解析式;
(Ⅲ)當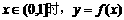 圖象上任意一點處的切線的傾斜角為
圖象上任意一點處的切線的傾斜角為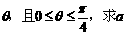 的取值范圍.
的取值范圍.
21.(本小題滿分12分)
已知點A、B的坐標分別是(-1,0),(1,0). 直線AM,BM相交于點M,且它們的斜率之積為-2.
(Ⅰ)求動點M的軌跡方程;
(Ⅱ)若過點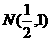 的直線l交動點M的軌跡于C、D兩點,且N為線段CD的中點,求直線l的方程.
的直線l交動點M的軌跡于C、D兩點,且N為線段CD的中點,求直線l的方程.
20.(本題滿分1 2分)
一群猴子第一天摘下若干個桃子,當即吃了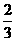 ,還不過癮,又吃了兩個. 第二天早上又將剩下的桃子吃掉
,還不過癮,又吃了兩個. 第二天早上又將剩下的桃子吃掉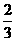 ,又吃了兩個. 以后每天早上都吃掉前一天剩下的
,又吃了兩個. 以后每天早上都吃掉前一天剩下的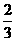 后還要吃兩個. 記
后還要吃兩個. 記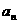 為第n天還沒吃時桃子的個數.
為第n天還沒吃時桃子的個數.
(Ⅰ)證明:{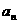 +3}是等比數列;
+3}是等比數列;
(Ⅱ)若到第七天早上想吃時,只剩下一個桃子了,求第一天共摘了多少個桃子?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com