
題目列表(包括答案和解析)
8.有5人排成一排照相,其中甲、乙兩人必須相鄰且不排在兩頭,則不同的排法共有
(A) 12種 (B) 18種 (C) 24種 (D) 36種
7.若 展開式的第5項等于
展開式的第5項等于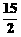 ,則x的值是
,則x的值是
(A)2 (B)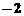 (C)
(C)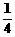 (D)
(D)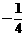
6.已知直線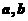 ,平面
,平面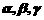 ,則使
,則使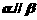 成立的一個充分條件是
成立的一個充分條件是
(A) (B)
(B)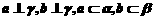
(C)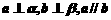 (D)
(D)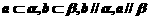
5.已知A、B、C三點共線(該直線不過原點O),若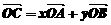 ,則
,則
(A)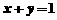 (B)
(B)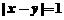 (C)
(C)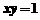 (D)
(D)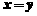
4.函數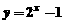 的圖像是
的圖像是

3.某中學有高一學生400人,高二學生300人,高三學生500人,現用分層抽樣的方法在這三個年級中抽取120人進行體能測試,則從高三抽取的人數應為
(A)40 (B)48 (C)50 (D)80
2.計算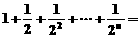
(A)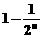 (B)
(B)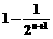 (C)
(C)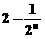 (D)
(D)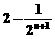
1.設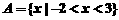 ,
, ,則
,則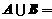
(A)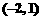 (B)
(B)
(C) (D)
(D)
21.(本小題滿分16分,第一小問4分,第二小問滿分6分,第三小問滿分6分)
設a為實數,設函數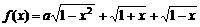 的最大值為g(a)。
的最大值為g(a)。
(Ⅰ)設t=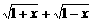 ,求t的取值范圍,并把f(x)表示為t的函數m(t)
,求t的取值范圍,并把f(x)表示為t的函數m(t)
(Ⅱ)求g(a)
(Ⅲ)試求滿足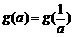 的所有實數a
的所有實數a
解:本小題主要考查函數、方程等基本知識,考查分類討論的數學思想方法和綜合運用數學知識分析問題、解決問題的能力。
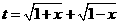
要使有t意義,必須1+x≥0且1-x≥0,即-1≤x≤1,
∴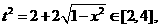 t≥0
①
t≥0
①
t的取值范圍是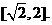 由①得
由①得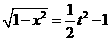
∴m(t)=a(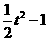 )+t=
)+t=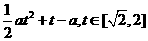
(2)由題意知g(a)即為函數 的最大值。
的最大值。
注意到直線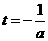 是拋物線
是拋物線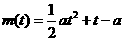 的對稱軸,分以下幾種情況討論。
的對稱軸,分以下幾種情況討論。
當a>0時,函數y=m(t), 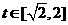 的圖象是開口向上的拋物線的一段,
的圖象是開口向上的拋物線的一段,
由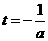 <0知m(t)在
<0知m(t)在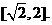 上單調遞增,∴g(a)=m(2)=a+2
上單調遞增,∴g(a)=m(2)=a+2
(2)當a=0時,m(t)=t, 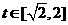 ,∴g(a)=2.
,∴g(a)=2.
(3)當a<0時,函數y=m(t), 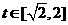 的圖象是開口向下的拋物線的一段,
的圖象是開口向下的拋物線的一段,
若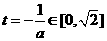 ,即
,即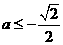 則
則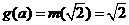
若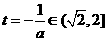 ,即
,即 則
則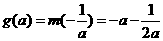
若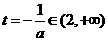 ,即
,即 則
則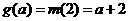
綜上有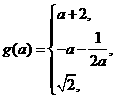
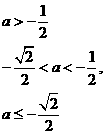
(3)解法一:
情形1:當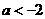 時
時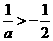 ,此時
,此時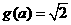 ,
,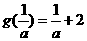
由 ,與a<-2矛盾。
,與a<-2矛盾。
情形2:當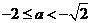
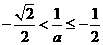 時,此時
時,此時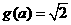 ,
,
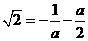 解得,
解得, 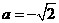 與
與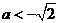 矛盾。
矛盾。
情形3:當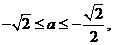
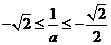 時,此時
時,此時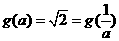
所以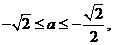
情形4:當 時,
時,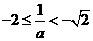 ,此時
,此時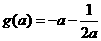 ,
,

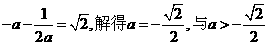 矛盾。
矛盾。
情形5:當 時,
時,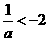 ,此時g(a)=a+2,
,此時g(a)=a+2,

由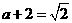 解得
解得 矛盾。
矛盾。
情形6:當a>0時, ,此時g(a)=a+2,
,此時g(a)=a+2, 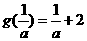
由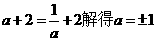 ,由a>0得a=1.
,由a>0得a=1.
綜上知,滿足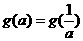 的所有實數a為
的所有實數a為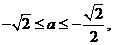 或a=1
或a=1
20.(本題滿分14分,第1小題滿分6分,第二小題滿分8分)已知函數f(x)=x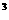 + x
+ x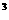 ,數列|x
,數列|x |(x
|(x >0)的第一項x
>0)的第一項x =1,以后各項按如下方式取定:曲線x=f(x)在
=1,以后各項按如下方式取定:曲線x=f(x)在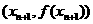 處的切線與經過(0,0)和(x
處的切線與經過(0,0)和(x ,f (x
,f (x ))兩點的直線平行(如圖)
))兩點的直線平行(如圖)
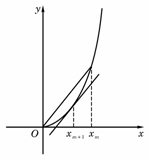 .
.
求證:當n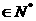 時,
時,
(Ⅰ)x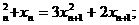
(Ⅱ)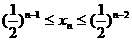
解:本題主要考查函數的導數、數列、不等式等基礎知識,以及不等式的證明,同時考查邏輯推理能力。
證明:(I)因為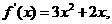
所以曲線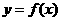 在
在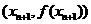 處的切線斜率
處的切線斜率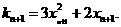
因為過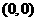 和
和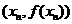 兩點的直線斜率是
兩點的直線斜率是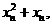
所以 .
.
(II)因為函數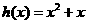 當
當 時單調遞增,
時單調遞增,
而
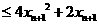
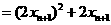 ,
,
所以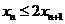 ,即
,即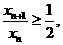
因此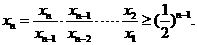
又因為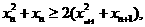
令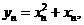
則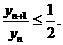
因為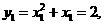
所以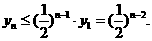
因此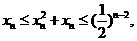
故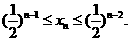
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com